Die letzte Dekade seit der Finanzkrise im Jahr 2008 war ein Paradies für Aktien-Sparer. Nachdem im Frühjahr 2009 mit ca. 53% Verlust der Tiefpunkt der Krise erreicht war, lag die durchschnittliche reale Rendite in den darauffolgenden 10 Jahren bei 15,2% pro Jahr. Die Volatilität war gleichzeitig historisch gering.
Es verwundert also nicht, dass in den letzten Jahren immer mehr Marktteilnehmer den Aktienmarkt als renditestarke Alternative zu inzwischen kaum noch auskömmlichen Festzinsanlagen für sich entdeckt haben. Für nicht wenige wird die aktuelle Corona-Krise der erste echte Markteinbruch sein. Und von diesen Anlegern werden die allermeisten bei einem kurzen Blick ins Depot viel Rot sehen. Die Krise hat innerhalb kürzester Zeit die Erträge der letzten Jahre brutal vernichtet. Der Aktienmarkt zeigt sich von seiner rauen Seite. Sind wir vorher lange Zeit bei ruhiger See und blauem Himmel gesegelt, befinden wir uns plötzlich inmitten eines stürmischen Orkans, bei dem ein Kaventsmann nach dem anderen auf Deck einschlägt. Einige Einschläge in den letzten Wochen waren dabei so heftig, dass jahrzehntealte, historische Rekorde gebrochen wurden.
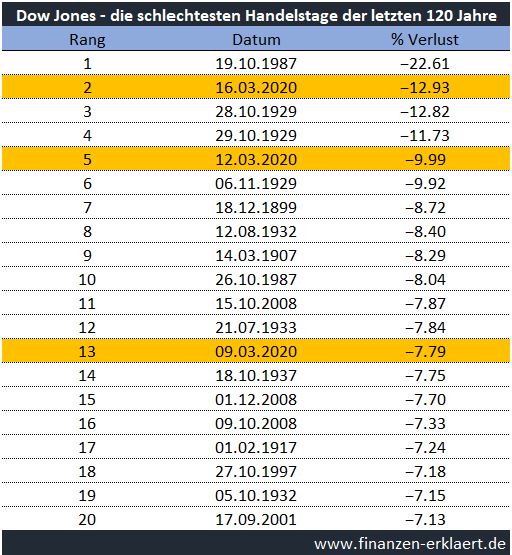
Innerhalb kürzester Zeit haben die Top 20 der schlimmsten Handelstage der letzten 120 Jahre gleich drei neue Einträge erhalten. Der bisherige erste Platz wurde zum Glück nicht von seinem Thron verdrängt. Schlimmer war in dieser Statistik nur der größte Crash aller Zeiten, die Weltwirtschaftskrise im Jahr 1929.
Kein Wunder also, dass junge Matrosen bei diesem Wellengang in Panik geraten, manch einer aus Verzweiflung sogar von Bord springt.
Odysseus würde wahrscheinlich seinen Depot-Zugang löschen
Ich persönlich empfehle jedem, dessen Nerven nicht stark genug sind diese Irrfahrt bis zum Ende durchzuhalten, wie Odysseus mit den Sirenen zu verfahren: er erteilte mit klarem Verstand seinen Mannen den Befehl, ihn vor Erreichen der Sirenen-Insel an den Mast seines Schiffes festzubinden. So konnte er dem Klang der Sirenen lauschen, ohne dabei zu riskieren den Verstand zu verlieren und ihrem Lockruf in den sicheren Tod zu folgen. Und genau so sollten es auch verunsicherte Privatanleger mit dem Depot halten. Denn bis vor kurzem warst Du sicherlich noch fest entschlossen, trotz Krise einfach Dein Ding weiter durchzuziehen. An diesem Vorhaben, beschlossen in ruhigen Zeiten klarer Gedanken, solltest Du unbedingt festhalten. Auch wenn die Sirenen des Marktes Dir eindringlich suggerieren, dass diesmal wirklich alles anders ist. Ist es nicht!
Wer nichts weiß muss alles glauben (Marie v. Ebner-Eschenbach)
Wer nicht so radikal wie Odysseus sein kann, der läuft Gefahr vor lauter Presse-Feuerwerk und Crash Propheten verrückt zu werden. Der beste Schutz ist Wissen über die Kapitalmärkte, in diesen Zeiten insbesondere Wissen über den Ablauf von Krisen an den Märkten. Denn es gibt ein Verhaltensmuster das seit über 120 Jahren stabil ist, und daher auch in dieser Krise fest eingeplant werden sollte: das schnelle Zurückschnalzen der Kurse nach heftigen Einbrüchen. Die folgende Tabelle zeigt die Bärenmärkte, d.h. Kursrücksetzer größer -20%, der letzten 120 Jahre. Neben der Information wie hoch der maximale Verlust war und wie lange die Krise insgesamt andauerte, liegt der Fokus der Daten auf der anschließenden Erholung. Und zwar habe ich ermittelt, wie hoch die durchschnittliche reale und nominale Rendite p.a. in den 5 bzw. 10 Jahren nach Eintritt des maximalen Verlustes war (gelber Bereich):
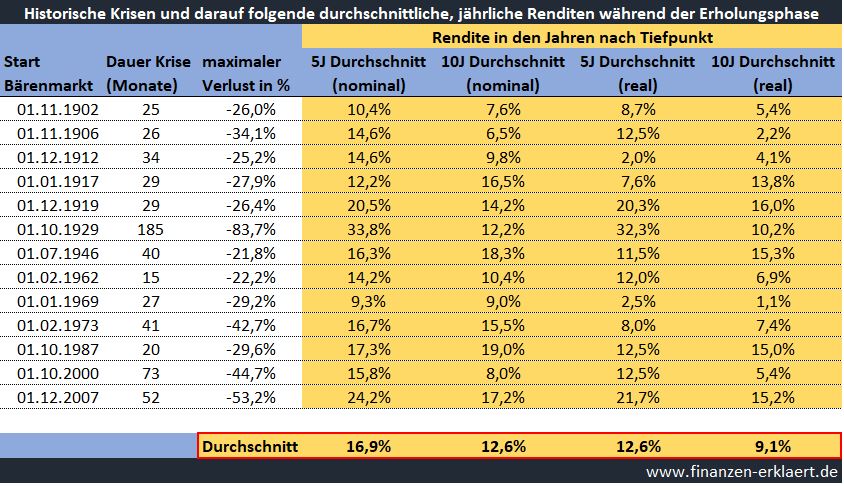
Das Ergebnis ist erstaunlich und erfreulich zugleich! Zeigt es doch, dass im Anschluss an die Krise üppige Renditen zu erwarten sind, die unsere Wunden schnell heilen lassen. In den ersten 5 Jahren nach Erreichen des Kurstiefs betrug in den darauffolgenden 5 Jahren die durchschnittliche, historische Rendite (pro Jahr!) 16,9% nominal bzw. 12,6% real. Und auch in den 10 Jahren nach Durchschreiten der Talsohle lagen die erzielten Renditen bisher regelmäßig weit über dem langfristig beobachteten Mittelwert. Weitere Fakten zu historischen Krisen findest Du ansonsten hier und hier.
Und genau so wird es diesmal auch wieder sein!
Wer daran nicht glauben kann, der hätte besser erst gar nicht in den Aktienmarkt investieren sollen. Denn basiert unser aller Business Case nicht auch zu großen Teilen auf dem Lindy Effekt? Dieser besagt, dass in der Vergangenheit beobachtete Muster sich desto wahrscheinlicher auch in der Zukunft fortsetzen, je länger diese bisher beobachtet wurden. Soll heißen, wir alle haben in dem festen Glauben daran investiert, dass sich die historisch beobachtete, durchschnittliche Rendite von 7% p.a. auch zukünftig einstellen wird. Weshalb sollte man dann annehmen, dass die Erholung nach der gegenwärtigen Krise anders als bisher verlaufen wird?
Wen die Historie nicht voll überzeugt, dem hilft vielleicht das hinter diesem Effekt stehende theoretische Konstrukt. Das folgende Modell erklärt, wieso es nach heftigen Krisen regelmäßig zu Überrenditen kommt. Der Chart zeigt auf der linken Achse drei Kursverläufe:
- Der theoretische Kursverlauf: dies ist der Verlauf ohne Krise. Hier gehe ich von der Grundannahme aus, dass der Aktienmarkt pro Jahr um 7% steigt. Daraus ergibt sich ein langfristig exponentielles Wachstum.
- Der gerechtfertigte Verlauf nach Krise: durch einen negativen Schock kommt es zu einem echten Verlust von 25%. Dieser ist dadurch begründet, dass der Schock den gegenwärtigen Substanzwert und / oder die zukünftig erwarteten Gewinne reduziert. Anschließend wächst der Markt wieder konstant mit 7% p.a., bleibt jedoch permanent unter dem Verlauf ohne Krise. Es handelt sich demnach um einen realen Wohlstandsverlust.
- Der tatsächliche Verlauf: Dies ist der Verlauf wie wir ihn tatsächlich beobachten. Neben dem gerechtfertigten Einbruch i.H.v. 25%, bewirken ungerechtfertigte Panikverkäufe einen zusätzlichen Einbruch von weiteren 25%. Der Unterschied zum gerechtfertigten Verlauf (2) ist jedoch, dass der Markt anschließend nicht einfach mit 7% p.a. weiterläuft. Stattdessen werden die durch Panikverkäufe verursachten Kursverluste im Zeitablauf wieder ausgeglichen. Und genau dieses Ausgleichen, die Rückkehr zum gerechtfertigten Verlauf, beschert uns die nach Kurseinbrüchen beobachteten Überrenditen.
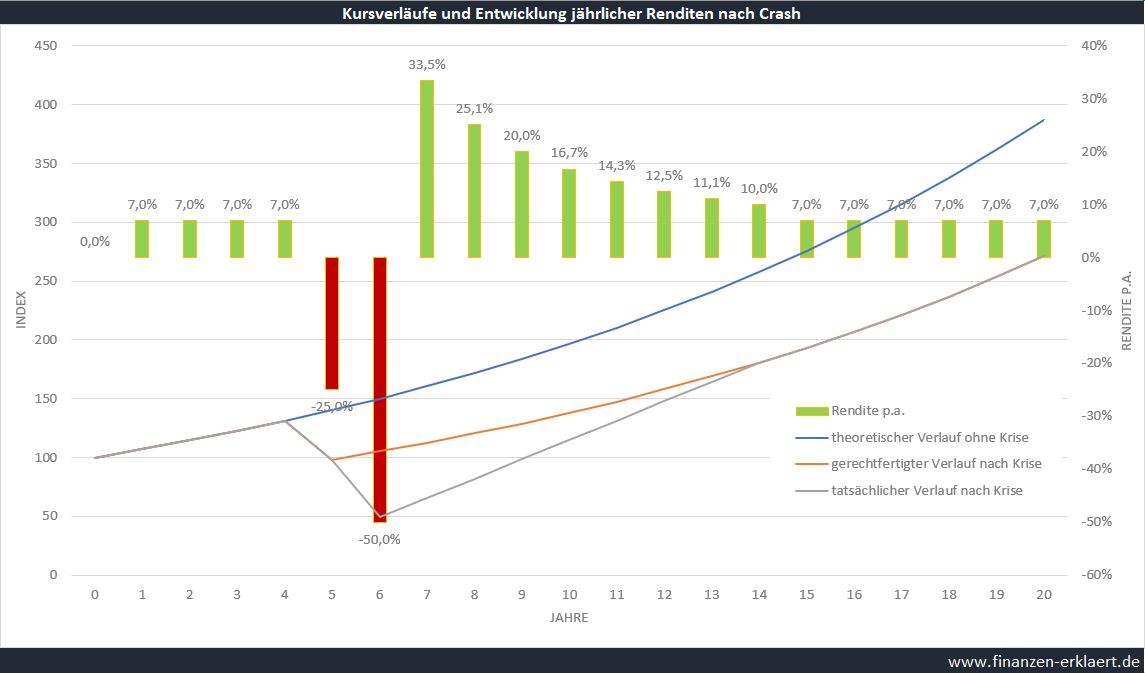
Auf der rechten Achse ist die Rendite p.a. abgetragen. Man sieht sehr deutlich, dass diese in den Jahren nach Erreichen des Tiefpunkts in der Krise überproportional hoch ist. Die hohen Wachstumsraten sind notwendig, um die Lücke zwischen dem tatsächlichen Verlauf und dem gerechtfertigten Verlauf wieder zu schließen. Und dass es auch in der aktuellen Krise wieder nur so vor Angst und Panik wimmelt, daran wird sicherlich niemand zweifeln.
Was bedeutet diese Erkenntnis für unsere Altersvorsorge und FIRE?
Die Königsdisziplin der privaten Altersvorsorge heißt FIRE, was für Financial Independence, Retire Early steht. Konkret geht es darum, noch vor Beginn der gesetzlichen Rente den Ruhestand zu beginnen, bzw. die Möglichkeit dazu zu haben (finanzielle Unabhängigkeit). Jeder der sich für dieses Thema interessiert hat bestimmt auch schon mal einen der vielen Rechner im Internet ausprobiert. In diesem Artikel präsentiere ich eine grafische Darstellung der Ergebnisse. Aus dieser Grafik lässt sich sehr leicht ablesen, wie lange es bei den gegebenen Parametern Sparquote, Rendite, Kapital und Sicherheitsbedürfnis dauert um die finanzielle Freiheit zu erreichen. Hier noch mal die Darstellung für eine jährliche Rendite von 7% p.a. inklusive Lese-Beispiel:
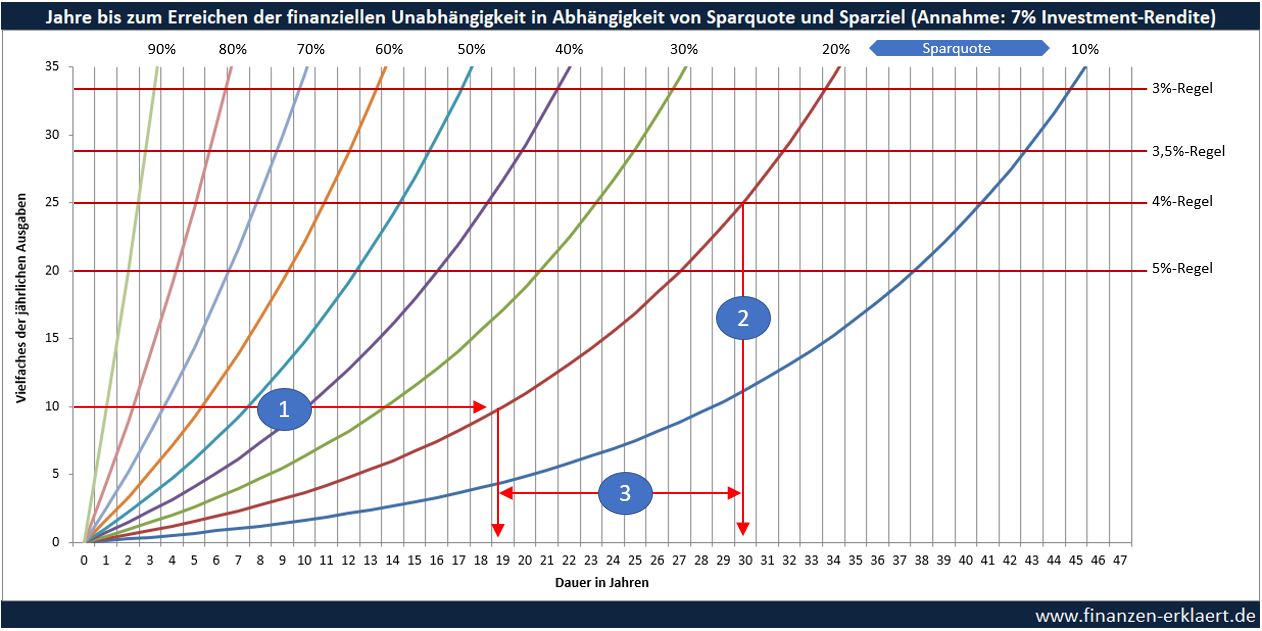
In dem Beispiel hat ein Sparer bereits 10 Jahresausgaben gespart. Die Sparquote beträgt 20%.
- Die 10-Jahresausgaben Kapitallinie schneidet die 20% Sparquotenkurve bei ca. 19 Jahren
- Die 20% Sparquotenkurve schneidet die Kapitallinie der 4%-Regel bei ca. 30,5 Jahren
- Die Differenz beträgt 30,5 – 19 = 11,5 Jahre. Der Sparer benötigt also noch weitere 11,5 Jahre bei 20% Sparquote, um finanziell frei zu sein.
Nach einer Krise ist anlog vorzugehen. Der wesentliche Unterschied liegt jedoch in der angenommenen Rendite und der Neubewertung der vorhandenen Ersparnisse. Letztere werden durch den Kurseinbruch reduziert sein. Jemand der vor der Krise bereits das 20-fache der eigenen, jährlichen Ausgaben angespart hatte, bleiben nach 50% Kurseinbruch nur noch Ersparnisse in Höhe der 10-fachen Jahresausgaben. Gleichzeitig steigt jedoch auch die jährliche Rendite während der Erholungsphase, wie oben gezeigt, signifikant an. Mit einer realen Rendite von 9% p.a. (= reale Rendite in den ersten 10 Jahren nach dem Crash, siehe Tabelle oben) sieht die Grafik wie folgt aus:
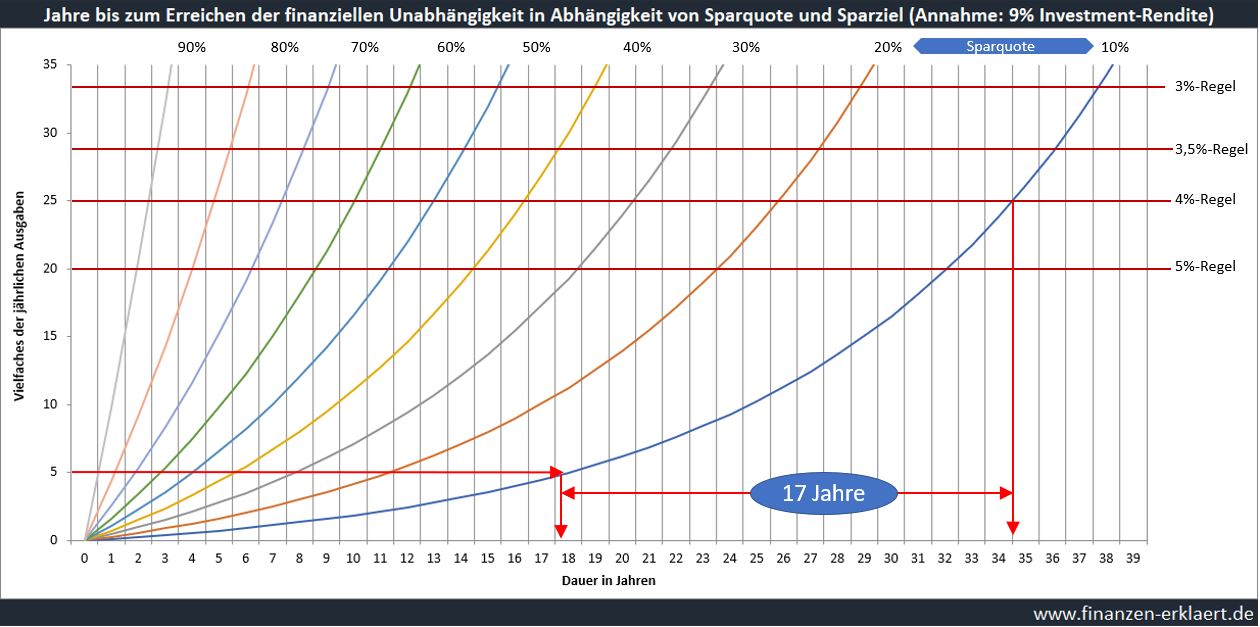
Wer also wissen will, um wie viele Jahre sich das Erreichen der finanziellen Unabhängigkeit durch die Krise verzögert, der arbeitet unmittelbar nach dem Crash mit dieser Grafik. Neben einem geringeren Vermögen und einer höheren Rendite für die nächsten 5-10 Jahre, kann auch eine veränderte Sparquote simuliert werden. Denn die Auswirkungen der Krise sind real. Manch einer wird nach der Krise ein verändertes Marktumfeld vorfinden oder einen neuen Job beginnen. Konsequenz kann eine reduzierte Sparquote sein, wodurch sich das Erreichen der finanziellen Unabhängigkeit zusätzlich verzögert.
Ein Lesebeispiel zur Grafik oben: der Sparer aus dem Beispiel oben hatte vor der Krise bereits 10 Jahresausgaben gespart. Nach einem Kurseinbruch von 50% beträgt der Depotwert nur noch 5 Jahresausgaben. Die Sparquote wird darüber hinaus wegen geringerer Einnahmen auf 10% reduziert. Zuvor hätte es noch 11,5 Jahre bis zur finanziellen Freiheit gebraucht. Jetzt mit den neuen Parametern beträgt die verbleibende Zeit noch 17 Jahre. Also insgesamt nur 6,5 Jahre mehr, und das obwohl sogar die Sparquote halbiert wurde! Mit konstanter Sparquote von 20% wäre das Ziel der finanziellen Freiheit nach dem Crash 13,5 Jahre entfernt, lediglich 2 Jahre später als ursprünglich geplant. Der Korrektur der Übertreibung sei Dank!
Eine ruhige Hand schützt vor dem finanziellen Super-GAU
Wer einen kühlen Kopf bewahrt und der Versuchung eines Panik-Verkaufs kurz vor dem vermeintlichen Weltuntergang wiederstehen kann, der wird weitestgehend unbeschadet aus der Krise hervorgehen. Denn die überdurchschnittlich hohen Renditen während der anschließenden Erholung haben einen starken Effekt. Ohne diese Kompensation gäbe es auch nicht die berühmte Regression zum Mittelwert.
Und wer trotz Krise und Depoteinbruch von den eigenen Ersparnissen leben will, der kann auch etwas aufatmen. Die folgende Tabelle zeigt, wie sich die sichere Entnahmerate nach einem Kurseinbruch verhält:
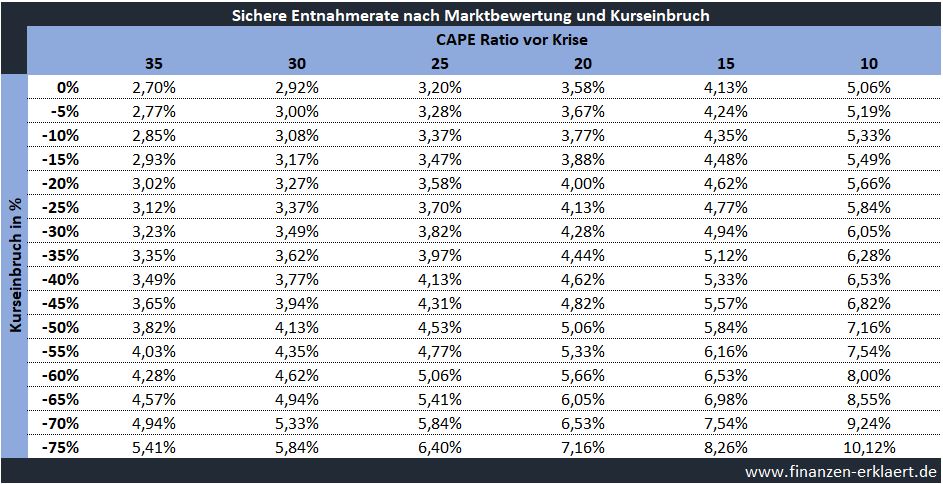
Beispiel: vor Ausbruch der Corona-Krise lag das Welt-CAPE bei ca. 25. Dem entsprechend lag die sichere Entnahmerate bei 3,2% p.a. Unter der Annahme eines 50%igen Kurseinbruchs verringert sich das CAPE auf 12,5. Die neue sichere Entnahmerate liegt dann bei 4,53%
Die gleichen Kräfte, die auch zu einer raschen Erholung unseres Portfolios führen, erlauben nämlich auch eine höhere sichere Entnahmerate nach einem Crash. Die genauen Hintergründe erfährst Du in diesem Artikel.
Und wenn alle Stricke reißen, bleibt noch das Vertrauen in das rheinische Grundgesetz: Et hätt noch emmer joot jejange!







Super Artikel, vielen Dank für die tollen Grafiken, welche das gelesene noch viel greifbarer machen. Werd den Blogbeitrag gleich nochmal lesen 😉
Toller Artikel!
Weiter so.
Viele Grüße
Tino
Ja, sehr schoene Arbeit, danke, Georg.
Oder pers. Vermoegen halt auf 200 Wochendurchschnitt (4 Jahresdurchschnitt) beziehen (sich geglaettet, aermer rechnen)?
pers. Depot-Vermoegen [€] x wGD200 vom pers. Index (zB MSCI ACWI IMI ETF-Kurs) / IST pers.Index = 25x Ausgabenziel [€]/a, funktioniert direkt, ohne den CAPE-Umweg, oder?
Bsp:
Fuer IE00B3YLTY66 bei Comdirect die Kursdaten heruntergeladen (woechentlich). Mit den Schlusskursen die fortlaufenden 200-Wochen GD berechnet (Mittelwerte)
Angenommen das Depot war Mitte Feb. 300k€ gross (4% entspraeche 12k oder 1k/mo, Ziel erreicht???), aber die Berechnung mit dem w200GD sagt:
ETF-Kurs 12.02.20 = 142,06€ w200GD = 111,35€ also ist das geglaettete Vermoegen auch nur 111,35€/142,06€ = 0,7838 x 300k€ = 235k€
Dein „passives Einkommen“ durch ETF-Verkaeufe koennte also realistisch erst 0,04 x 235k€ = 9,4k€ pro Jahr (vor Steuern und Abgaben) sein.
Inzwischen sind die Boersen abgestuerzt. Jetzt ist das Depot nur noch 300k€ * 101,9(18.03.20) / 142,06(12.02.20) = 215k€ gross.
Wie sieht es jetzt aus?
ETF-Kurs 18.03.20 = 101,90€ w200GD = 112,01€ also betraegt das geglaettete Vermoegen 112,01€/101,90€ = 236k€ (aha, sogar etw „mehr“ geworden, trotz Crash)
Dein „passives Einkommen“ durch ETF-Verkaeufe koennte also 0,04 x 236k€ = 9,4k€ pro Jahr (vor Steuern und Abgaben) sein (= nix passiert!).
Fazit: eine Glaettung (zB 200-Wochen-GD) hilft ein realistisches Bild auf dein Vermoegen zu bekommen und bewahrt dich vor zu optimistischer oder zu pessimistischer Sichtweise entlang der Boersenzyklen.
Dadurch bist du in Euphorien geerdet und in Depressionen ermutigt? Komplizierte CAPE oder andere Bewertungsmasstaebe sind unnoetig?
LG Joerg
Hi Joerg,
die Idee zu der impliziten Bewertung hatten wir ja auch schon mal an anderer Stelle diskutiert: https://www.finanzen-erklaert.de/entnahmestrategien-optimieren-bessere-rente-dank-cape-ratio/
Ich gebe dir recht, man kann auch auf das CAPE Ratio verzichten und statt dessen die Bewertung über den eigenen Portfolio-Schnitt errechnen. Man bräuchte sehr gute eigene Aufzeichnungen, und müsste Zukäufe, Verkäufe, Dividenden etc in der Berechnung korrigieren.
Oder man hat einfach nur ETFs in z.B. MSCI World oder EM und beschafft sich eine Kurshistorie, das wäre sicherlich am sinnvollsten.
Ich habe mich im Anschluss an die Diskussion auch kurz mit der Idee befasst. Um Ergebnisse zu erhalten die mit der CAPE Lösung vergleichbar sind, musste ich auf eine 20-jährige Historie abstellen. Du kannst dann z.B. mit der Formel SER=0,058x^-0,689 eine sichere Entnahmerate ermitteln, wobei x einfach dem aktuellen Kurs im Verhältnis zum Mittelwert der letzten 240 end-of-month Werte des Total Return Index entspricht. Diese Formel lässt sich bestimmt wie auch meine CAPE-Formel noch etwas „verschönern“ ohne das Ergebnis wesentlich zu beeinträchtigen. Die benötigte Historie ist also etwas länger, aber durchaus machbar. Am Ende Geschmackssache ob man lieber selber rechnet oder sich die Arbeit sparen und fremden Daten vertrauen will.
Bei Interesse kann ich Dir gerne ein Excel zukommen lassen indem ich Deine Idee simuliere und wir können noch mal ausführlicher drüber quatschen.
Gruß
Georg
Danke, Georg,
ja, das finde ich interessant. Siehst du meine Email-Adresse, die ich jedesmal brav in die Kommentarfunktion eingebe? Allerdings sind meine xls-Kenntnisse verglichen mit Dir eher Grundschul-Niveau 😉
Meinst du 20Jahres GD? Das waere ja demotivierend lang? Hoffte, schon mit 4Jahres GD vernuenftige Glaettung zu erhalten …?
„Man bräuchte sehr gute eigene Aufzeichnungen, und müsste Zukäufe, Verkäufe, Dividenden etc in der Berechnung korrigieren.“ Das verstehe ich nicht?
Ich brauche nur einen Index, der meinem Ist-Depot-Bestand entspricht, oder? Das meintest Du mit dem naechsten Satz, „Oder man hat einfach nur ETFs in z.B. MSCI World oder EM und beschafft sich eine Kurshistorie, das wäre sicherlich am sinnvollsten.“ oder?
Ja, genau, mit 3 ETF als Index (MSCI WORLD, MSCI EM, MSCI World SmCap) kann fast jedes Depot einfach abbilden/Korrekturfaktor berechnen (ggfls noch eine Prise Stoxx600, etc).
LG Joerg
Hi Joerg,
ich hab jetzt noch was viel besseres gefunden: und zwar habe ich gesehen, dass man über OneDrive auch Excel Dateien in einen Blog einbinden kann. Ich habe das mal mit dem oben erwähnten Excel auf folgender Seite testweise aufgesetzt: https://www.finanzen-erklaert.de/excel-tests/
In die gelbe Zelle kannst du die Anzahl Jahre bei der Durchschnittsberechnung eintragen. Wenn Du zb auf 10 Jahre runtergehst, dann sieht man wie die Punktewolke nach unten sackt. D.h. die resultierenden Entnahmeraten werden geringer, das Ergebnis ist nicht optimal.
Unten rechts in der Excel Box befindet sich zudem ein Download link.
Auf den ersten Blick finde ich diese Funktion Excel in den Blog einbetten zu können echt klasse. Ich denke davon werde ich zukünftig noch häufiger Gebrauch machen.
Gruß
Georg
Danke, sieht lustig aus, zB bei Eingabe von 30 Jahren, aber das ist fuer mich nicht nachvollziehbar.
Sollte mit 30 Jahren nicht eine Super-Glaettung herauskommen? Irgendwie tut sich wenig mit den Ausreissern nach unten im unteren Diagramm (sollten die nicht von 2,5% Entnahme Richtung 4 ansteigen?) und das obere Diagramm macht lustige mehrgipflige Wellenreiter-Kapriolen? LG Joerg
Der maximal mögliche Wert ist 20, alles darüber ergibt nur quatsch (das ist nur ein Test der heute von mir entdeckten Excel Funktion, ohne jegliche Sicherungen etc.)
Wenn Du von 20 immer weiter runter gehst, siehst Du auch wie das R2 immer weiter runter geht. Es gibt dann keinen signifikanten Zusammenhang mehr zwischen den historischen sicheren Entnahmeraten und dem Bewertungskoeffizienten. Es könnte sogar sein, dass das Ergebnis mit einem noch längeren Durchschnitt noch besser wird. Um dies zu überprüfen müssten die Historie der Marktdaten entsprechend verlängert werden.
Moin Georg,
interessehalber: was passiert eigentlich, wenn man „4“ Jahre in das Formel Feld eingibt (mit deinen eigenen Worten erklaert)?
Was ich mir wuenschen wuerde, ist ja, mit 200-Wochen-GD-Werten bzw bei dir mit 46-Monats-Durchschnitten zu rechnen, anstatt mit den Orginalwerten. Dann muesste sich die sichere Entnahmerate in einem viel engeren Korridor bewegen? Oder?
Ich vermute bei Deinem Verfahren wird etwas anderes gemacht (hab‘ ich nicht genau verstanden, was).
LG Joerg
Moin Joerg,
wenn du 4 eingibst, dann wird der Parameter auf der x-Achse mit einem 4-jährigen Durchschnitt bestimmt. Grundlage sind monatliche Daten.
Das Diagramm ist das gleiche wie auch in dem CAPE Artikel. Nur dass das CAPE Ratio hier durch einen alternativen Bewertungsparameter ersetzt wurde. Nämlich historischer Durchschnitt / aktuelle Marktbewertung. Mit dem Parameter in der gelben Zelle steuerst du durch die Länge des Durchschnitts also die Berechnungsmethodik.
Auf der y-Achse befinden sich die historischen sicheren Entnahmeraten. Man sieht, dass bei einem längeren historischen Durchschnitt die Aussagekraft deutlich zunimmt. Das R2 zwischen Parameter und historischer Entnahmerate nimmt deutlich zu. Gleichzeitig sieht man auch sehr schön wie sich dieser Zusammenhang grafisch formiert. Die Punktewolke wird gestreckt und angehoben. Die daraus abgeleitete Entnahmeformel würde also bei gegebenen Bewertungsparameter stets eine höhere sichere Entnahmerate liefern. Daher ist das Ergebnis auf Basis eines längeren Durchschnitts besser.
Vielleicht wird es sogar noch besser wenn der Durchschnitt über 25 oder 30 Jahre bestimmt wird? Müsste man ausprobieren. Was ich sagen kann ist, dass bei 20 Jahren die gleiche Performance wie mit einer CAPE basierten Regel erreicht wird.
Gruß, Georg
Danke Georg,
das untere Diagramm mit den sicheren Entnahmeraten scheint sich nie zu veraendern, egal welche Jahreszahl ich eingebe? – aber egal.
das obere Diagramm zeigt eine Verschiebung der Punktewolke nach rechts, ok.
Ich fixiere jedoch jeweils die zwei „schlimmsten“ Punkte in der Wolke (so bei 2,5-2,8% Entnahmerate?) die bleiben immer auf diesem Niveaeu?!
Bei einer Berechnung, wie ich sie vorgeschlagen habe (Transformation der Orginalwerte auf deren 4Jahres-GD und Berechnung mit diesen), sollten die min. und max. Werte (Punkte) fuer die Entnahmerate jedoch deutlich zur Mitte schrumpfen?! Das scheint fuer deine Min/Max nicht zu gelten?
Deshalb vermute ich, dass irgendetwas bei deiner Berechnungsart substanziell verschieden ist (von meinem Vorschlag)?
LG Joerg
Ich glaube ich verstehe jetzt woher das Missverständnis kommt. Und zwar betrachte ich die sichere Entnahmerate als gegeben. Im Excel findest du in der Spalte J für jeden Monat der letzten 120 Jahre die maximal mögliche sichere Entnahmerate für einen 60-jährigen Entnahmezeitraum. Diese fliesst also als Input in meine Berechnung ein, und ist daher nicht veränderlich. Daher bleiben auch die Extrempunkte natürlich an ihren Stellen.
In einer klassischen Entnahmeraten-Rechnung würde man jetzt den kleinsten Wert wählen und wäre an der Stelle fertig. Ich habe jedoch in dem CAPE Artikel gezeigt, dass durch die Berücksichtigung der Marktbewertung eine sichere Entnahmerate gewählt werden kann, die i.d.R. über dem gesamthaften Minimum liegt.
Jetzt ersetzen wir CAPE durch einen neuen Bewertungsparameter, der sich einfach aus der Historie ergibt, so wie von dir vorgeschlagen. Und wiederholen anschließend die Prozedur der Formelfindung (siehe den CAPE Artikel für die genaue Vorgehensweise). Dabei stellt sich heraus, dass die Verwendung des 20y Durchschnitts das beste Ergebnis liefert. D.h. auf Basis des resultierendes Scatter-Plots lässt sich eine gute Funktion zur Ermittlung der sicheren Entnahmerate schätzen.
Was man nicht machen kann ist wie du im ersten Kommentar eine feste Formel vorgeben. 4% mal irgendwas? Woher kommen die 4%? Woher der 200 Wochen GD? Das sind alles Parameter die es zu ermitteln gilt, keine festen Vorgaben. Ich denke hier liegt der Fehler. Fest vorgegeben sind nur die sichere Entnahmeraten und die Ausprägungen des Bewertungskriterium, alles andere muss darauf aufbauen ermittelt werden und nicht andersherum.
Zum 2. Diagramm das sich nicht verändert: ich habe mir wie gesagt hier nicht viel Mühe gegeben und dir einfach die Datei so wie sie ist hochgeladen. Es sind gewisse Excel Kenntnisse notwendig, dann lassen sich die Formeln nachvollziehen und man versteht was wie zusammenhängt. Ich bin jetzt einfach mal davon ausgegangen, dass bei dir diese Kenntnisse vorhanden sind. Wenn du dir die Datenquelle des Diagramms ansiehst, dann wirst du sehen dass dieses den Zusammenhang zwischen CAPE und sicherer Entnahmerate darstellt. Daher natürlich auch kein Impact wenn man die Durchschnittsberechnung modifiziert.
Vielen Dank fuer deine Geduld mit mir und Dein Erklaeren!
Du hast vollkommen recht, die 4% kommen aus dem hohlen Bauch (OK, nicht ganz, die gaanz langfristige Realrendite ist ca. bei 5% p.a., bei gaanz langer Glaettung koennte man also vielleicht 4% „sicher“ entnehmen, 1% Puffer) und die 200 Wochen GD kommen aus der Charttechnik, oft als langfristiger, meist haltender Abprall-Region zwischen Kurs und GD (Jedenfalls bei den kuerzeren Baissen der letzten 30 Jahre in zB MSCI World).
Ich habe nicht deine Skills, deshalb freue ich mich ueber Deine Optimierung von Entnahme und GD.
Noch ein letztes zu: „Im Excel findest du in der Spalte J für jeden Monat der letzten 120 Jahre die maximal mögliche sichere Entnahmerate für einen 60-jährigen Entnahmezeitraum. Diese fliesst also als Input in meine Berechnung ein, und ist daher nicht veränderlich.“
Genau da bin ich mir unsicher: Ich meine, wegen des SoRRs muessten sichere Entnahmeraten auf den zB w200GD berechnet (statt auf den orginalen Monatswerten wie bei Dir) zu etwas hoeheren per se Entnahmeraten fuehren!?, weil ja in Baissen automatisch von einer hoeheren und in Haussen von einer niedrigeren Basis ausgegangen werden wuerde?
Oder ist das ein Denkfehler?
LG Joerg
Die sichere Entnahmerate ist bei gegebener Rendite-Reihenfolge eindeutig ermittelbar. Es gibt nur eine Lösung. Du kannst es gerne selbst mit den Raten aus dem Sheet testen: einfach die Rate durch 12 teilen, und dann jeden Monat dementsprechend entnehmen. Das verbleibende Kapital rentiert im weiteren Zeitablauf analog zum Markt (der der Berechnung zugrunde liegt), nach 60 Jahren wirst du exakt bei 0 landen.
Wer konservativ sein will, sich aber nicht pauschal für die niedrigste aller Entnahmenraten entscheiden will, kann versuchen sich anhand weiterer Variablen zu orientieren, so wie z.B. hier an der Marktbewertung. Deine Idee das CAPE durch die implizite Bewertung zu ersetzen ist gut und funktioniert auch. Die Frage ist mit welcher Bewertungsvariablen kann ich wieviel von der Streuung der historischen Entnahmeraten erklären. Und da zeigt sich, dass ein 20 jähriger Mittelwert so gut ist wie CAPE, welches eine 10 jährige Earnings-Historie benötigt.
Das kannst du z.B. überprüfen indem du durch den 2. Chart ebenfalls eine Regressionsgerade legst. Du wirst sehen, dass bei 20y Durchschnitt das R2 dem mit CAPE entspricht.
Abschließend gilt es eine Funktion zu finden, welche den unteren Rand der Punktewolke beschreibt. Bei 20-jährigen Durchschnitt funktioniert z.B. 6%/Wurzel(x^3) mit x = 20y Schnitt / Preis ganz gut.
Danke Georg,
die Daten aus der xls konnte ich ueberkopieren, Formeln kommen aber keine mit …
Deshalb weiss ich jetzt nicht, wie die 60y SER berechnet wurde/kann es nicht selber.
(evtl kann ich es mit deiner Datei/Formeln?)
Allerdings verstehe ich deine Aussage nicht: „Die sichere Entnahmerate ist bei gegebener Rendite-Reihenfolge eindeutig ermittelbar. Es gibt nur eine Lösung.“
Die Renditereihenfolge auf den w200GD-transformierten Daten waere doch anders, oder? und bei einer Datenglaettung gaebe es viele Loesungen(je nach Glaettung, 4y 6y 8y usw), oder?
In der Evolution meines Verstaendnisses ist es ja nun suboptimal einfache Monats-Schlusskurse zu nehmen, weil ja diese ueber- oder untertrieben sein koennten. Durch die Rechnung auf geglaetteten Daten umgeht man dies (aber was ist die optimale Glaettung? die, bei der die sichere Entnahmerate maximiert werden wuerde. 60y ist vielleicht etwas ueberoptimistisch, 50y oder 40y duerften fuer mehr Leute interessant sein?).
Bildlich gesprochen: eine Punktewolke der Entnahmeraten, die eine geringe Streuung zeigt, und ein moeglichst hohes Minimum.
Oder was meinst Du?
LG Joerg
Hi Joerg,
die 60y SER habe ich in einer andere Datei berechnet und dann hier reinkopiert. Von daher korrekt, dass du keine Formel siehst.
Irgendwie verstehe ich glaube ich den Gedanken mit der Datenglättung nicht. In der Realität müsste sich dein Depot ja auch den realen Renditen und nicht irgendwelchen geglätteten Renditen stellen. Von daher muss man die SER auch mit diesen echten Renditen ermitteln.
60y ist schon sehr safe. Aber auch dieses Thema adressiere ich in dem CAPE Artikel. Man kann die Lage der Funktion sehr leicht verschieben. Wer richtig sicher sein will muss bei der CAPE Formel zB 14% statt 16% verwenden. Und ich zeige ja auch im Backtesting wie verschiedene Parameter im Zeitablauf performen.
An der Streuung der Entnahmeraten wirst du nichts ändern können, denn diese sind wie gesagt gegeben.
Gruß
Georg
Lieber Georg,
„Irgendwie verstehe ich glaube ich den Gedanken mit der Datenglättung nicht. In der Realität müsste sich dein Depot ja auch den realen Renditen und nicht irgendwelchen geglätteten Renditen stellen. Von daher muss man die SER auch mit diesen echten Renditen ermitteln.“
Das ist ja der wesentliche Trick: du rechnest deinen Depotstand bereinigt zum Verhaeltnis deines Ziel-Index aus! Dadurch umgehst Du Unter/Ueberbewertung des momentanen Ist-Wertes.
Man kann sich ja von zwei Seiten dem Entnaheme-Problem naehern: die Masse versucht auf einem wilden Zick-Zack-Kurs (Depot-Boersenwert) eine volatile Entnahmerate mit CAPE oder Floor/Ceiling, etc zu zaehmen. Viel einfacher und ohne externe Parameter (nur geglaetteter Kurs) rechnet man sich entsprechend aermer (Uebertreibung) oder reicher (Baisse). Das ist mE viel mehr straight-forward?
LG Joerg
Das ist bei einer einfachen Entnahmestrategie ohne Floor / Ceiling im Endeffekt exakt das gleiche.
Entnahmebetrag = Portfolio x Entnahmerate
Ob du jetzt das Portfolio oder die Entnahmerate adjustierst ist wurst.
Es gibt nur eine gültige Lösung für das Endergebnis (absoluter Entnahmebetrag), aber mehrere Lösungswege.
Ja, hat mit Floor/Ceiling nix zu tun, stimmt.
„Ob du jetzt das Portfolio oder die Entnahmerate adjustierst ist wurst.“
Da bin ich mir nicht sicher, weil die Volatilitaet des Portfolios (Wertschwankungen) groesser ist, sollte das SoRR entlang des Entnahmepfades groesser sein als auf einem geglaetteten Depotwert?
Ausserdem ist jederzeit eine einfache(re) neue Berechnung/Adjustierung der Entnahmerate moeglich (on the fly)? Weil irgendwie muss ich ja schauen, ob es gerade eher ueber- oder unterbewertet ist, wenn ich in den Sack haue(aehm, mit Entsparen anfange)?
Wir koennen gerne telefonieren, habe dir Nr gemailt.
Gerne wuerde ich an Bsplen selber rechnen (oder wenn es fuer dich keine Muehe ist Du?),
wie/ob auf versch. geglaetteten S&P Daten die Entnahmeraten variieren?
LG Joerg
Nach Beschaeftigung mit den Rohdaten von der MSCI.com Seite (MSCI ACWI IMI, Net, USD) vom Mai.1994 bis Feb.2020 und mehrer GDs (24m, 36m, 48m, 60m, 72m) in Excel:
Der „schlimmste“ Beginn fuer einen Entnahme-Start war der 31.03.2000, dort war ein lokales Hoch im MSCI ACWI IMI.
Unterwasser-Phase Apr.2000-Dez.2005 und dann Nov.2007-Jun.2013. Die 4% Entnahme vom Start-Vermoegen + 1,5% p.a. Inflationsausgleich haetten trotzdem bisher geklappt (Feb.2020), aber das verbliebene Vermoegen waere ab Feb.2020 unter den Faktor 100 gefallen (= 1 Monatsentnahme ist mehr als 1/100 vom Restvermoegen, also zB 1.000 EUR monatliche Entnahme bei Restvermoegen von unter 100k€), was ich pers. etw. als rote Linie betrachte.
Alle GD-Verfahren wurden dann mit alternativen Entnahmeraten zu diesem Zeitpunkt (Mrz.2000) verglichen.
Fazit:
Die hohle-Bauch-Idee mit 4% Entnahme auf einem woechentlGD200 ist zu konservativ(zu wenig wird entnommen, das verbleibende Kapital waechst zu stark).
Ja, Georg hat recht, es gibt beim Rueckblick auf den Entnahmepfad jeweils nur eine optimale Entnahmerate (analog zu einem Tilgungsplan).
Die Betrachtung gleitender Durchschnitte – statt der Kurse direkt – macht keinen Unterschied bezueglich der Entnahme-Hoehe oder des SoRR.
Es ist egal, ob man die SWR direkt auf den Kursen bestimmt oder „ueber Bande spielt“ mit GDs.
Die einzige Hilfe von GDs besteht darin, den Abstand des momentanen Depotwertes von den GDs zu erfassen und so fuer sich selbst zu beurteilen, ob man eher mit 4% Entnahmerate startet (hohe Bewertung, Depot-Wert ziemlich ueber dem GD) oder sogar mit 6% (niedrige Bewertung, Depotwert unter dem GD).
Eine gute Einschaetzung hat bereits der 36mGD gegeben, 48mGD noch konservativer und beim 72mGD waren die Zeiten vom Depot-Wert unter dem GD sogar sehr klein/irrelevant.
Ich hoere gerade einen empfehlenswerten Podcast von Michael Kitces auf ChooseFI (engl) google: Michael Kitces ChooseFI 171 flexible spending rules for early retirees:
– 4%-Regel war im Kontext damals revolutionaer, weil alle mit ueberoptimistischen 6-8% rechneten.
– fast immer (>95%) in der Historie konnte man aber mehr als 4% entnehmen
– er empfiehlt mit 5% zu starten und dann auf dem Weg (alle 3 Jahre) zu pruefen und ggfls zu adjustieren
Bei diesen Adjustierungen koennte die Betrachtung von Index-GDs helfen, die ueberwiegend deiner Asset-Allokation entsprechen, ohne auf eine Bewertungskennziffer angewiessen zu sein (zB CAPE)?
LG Joerg
Danke für den Hinweis mit dem Podcast, werde ich mir definitiv abhören!
Ich persönlich mag keine Entnahmestrategien bei denen der Entnahmebetrag schwankt. Wenn, dann soll dieser höchstens im Zeitablauf zunehmen, aber niemals abnehmen. Ohne harte Untergrenze kann man nicht vernünftig planen finde ich.
Eine gute Möglichkeit dieses Ziel zu erreichen besteht darin bei jedem Entnahmetermin zu rechen: ist aktuelles Portfolio x aktuell gültige Entnahmerate > bisheriger Entnahmebetrag? Falls ja, auf höheren Entnahmebetrag wechseln, falls nicht bleibt alles beim alten.
Mit diesem Trick lassen sich Portfolios sehr effektiv entsparen.
Hallo,
schöner Artikel und klingt auch plausibel, aber ich bin mir da nicht sicher. Ich würde mir auch mal die Crashs 1929 mit Ursache und Wirkung anschauen und 1989 Japan, da war es nicht so viel mit Recovery nach 5 Jahren. Die Zinsen sind noch nicht normal!
Wenn die Kurse zu hoch sind, warum sollen sie anschließend die durchschnittliche Rendite erzielen. Und wenn sie nach einen Crash immer noch zu hoch sind? Vielleicht sind die 7% nicht die „Wahrheit“. Die durchschnittliche Rendite zu berechnen ist schwer, weil die Bewertung am Start- und Endzeitpunkt identisch sein muss. Aber zu welchen Zeitpunkten war das der Fall?
Was war die durchschnittliche Zeit für einen Bärenmarkt, abgesehen 1987? Wann ist es vorbei? Wenn es am Ende -90% gibt ist verkaufen bei -40% gar nicht so schlecht. So lange alle glauben es ist vorbei, ist es vielleicht nicht. Wenn noch keiner in Panik verkauft hat, gab es keine Panik. Wenn alle sagen, dass wird schlimmer als die Finanzkrise, mehr Schulden, härtere Rezession, etc., warum sollen die Kurse nicht noch tiefer fallen als damals? Oder wenigstens nur prozentual?
Lange Rede, ich weiß es auch nicht, habe bei 8.600 die ersten Käufe gemacht, bei 9.600 aber wieder verkauft etwas verkauft.
Grüße, Alex
PS: Bill Ackman hat es gewusst und 2,6 Mrd. verdient. John Paulsen Mrd. bei der Finanzkrise. Fisher Investments hat vor der DotCom Krise gewarnt. Einer weiß es immer… 😉
Hi Alex,
in der Tabelle zu den Recoveries sieht man ja, dass es nicht immer im Anschluss steil nach oben geht. Besonders auffällig ist dies in den 70er Jahren, da in dieser Zeit die Inflation so hoch war (Ölpreiskrise).
Eine Sicherheit gibt es also nicht, nur Tendenzen. Wie bei allem an der Börse.
Was meinst Du genau mit „die Bewertung muss identisch sein“?
Wenn Du Dich für die Merkmale von Bärenmärkten interessierst, dann schau habe ich hier einige Daten zusammengetragen: https://www.finanzen-erklaert.de/corona-virus-nur-eine-korrektur-oder-der-anfang-eines-baerenmarktes/
Als ich die Story mit den 2,6 Mrd gelesen habe, habe ich das gleiche wie du gedacht. Aus meiner Sicht Zufall & Glück. Vermutlich hat er auf einen ganz anderen Crash gehofft, und dann kam halt das dazwischen. Und über die die ein paar Mrd verloren haben redet keiner 😉