Kann man mit einer Put-Option die Entnahmestrategie optimieren?

Dieser Artikel ist etwas Besonderes. Wir werden die bisher erarbeiteten Entnahmestrategien um den Einsatz von Derivaten erweitern. Konkret geht es darum zu Beginn der Entnahmephase eine Put-Option zu erwerben, um sich so vor dem berühmt berüchtigten Rendite-Reihenfolgerisiko zu schützen. Absolut spannend!

Doch der Reihe nach. Dieser Artikel hat den Anspruch ein komplexes Thema einer breiten Leserschaft nutzbar zu machen. Wir werden daher kurz darauf eingehen müssen wie genau eine Put-Option funktioniert. Anschließend ein besonderer Leckerbissen für alle Finanz-Nerds: Wir führen eine historische Simulation der Put-Strategie ab 1929 durch! Jeder der sich bereits tiefer mit dem Thema Optionen befasst hat, wird sich fragen, wie dies möglich sein soll. Denn das mit dem Nobelpreis ausgezeichnete Black-Scholes Modell zur Bepreisung von Optionen gibt es erst seit den 70er Jahren. Dementsprechend sind die benötigten Marktdaten für die Zeit davor nicht verfügbar, man muss improvisieren! Abschließend schauen wir uns die Effekte der Put-Strategie auf die sichere Entnahmerate an. Ich kann an dieser Stelle schon mal verraten, dass die Ergebnisse wirklich vielversprechend sind.

Eine Put-Option ist eine Versicherung gegen Kursverluste

Eines der ersten Themen dem man begegnet, sobald man sich über Entnahmestrategien informiert, ist das Renditereihenfolgerisiko. Bei einer Einmalanlage über einen längeren Zeitraum spielen Kursschwankungen keine Rolle. Es geht nur um das Endergebnis und die daraus errechnete durchschnittliche Rendite. Wer hingegen von seinem Kapital entnimmt, für den ist die Reihenfolge der Renditen relevant. Bei der Entnahme ist es vorteilhaft, wenn die Renditen am Anfang der Entnahmephase höher ausfallen als zu deren Ende. Der Worst-Case ist dementsprechend das genaue Gegenteil: Ein Crash unmittelbar zu Beginn der Entnahmephase. Eine wesentliche Aufgabe von Entnahmestrategien ist es das Renditereihenfolgerisiko zu reduzieren und so eine höhere Entnahme bei gleichem Kapitalstock zu ermöglichen. Wir halten fest:

>Kernaussage Nr. 1: ein Crash unmittelbar zu Beginn der Entnahmephase ist der Worstcase

Was liegt daher näher als sich einfach gegen das Risiko eines Crashs zu Beginn der Entnahmephase zu versichern? Ähnlich wie bei einer Unfallversicherung zahlt man eine kleine Prämie für ein gering wahrscheinliches Ereignis. In der Mehrzahl der Fälle tritt das unwahrscheinliche Ereignis nicht ein, und die Versicherungsprämie ist verloren. Tritt das versicherte Ereignis aber doch ein, dann beträgt die Auszahlungssumme der Versicherung oft ein Vielfaches der ursprünglichen Prämie.

Genau so muss man sich eine Put-Option vorstellen. Eine Put-Option schützt das Portfolio im Falle eines Crashs vor Wertverlust. Kommt es zum Crash, dann erhält der Besitzer der Put-Option eine Zahlung, die den Wertverlust des Depots (teilweise) ausgleicht. Tritt dagegen kein Crash ein, wird die Versicherung nicht benötigt und die Option verfällt wertlos.

>Kernaussage Nr. 2: eine Put-Option gewinnt im Falle eines Crashs an Wert und mindert so den Worstcase

Ob sich der Kauf einer solchen Versicherung lohnt, hängt davon ab wie hoch der Preis dieser Versicherung ist. Und der Preis hängt wiederum von der subjektiven Eintrittswahrscheinlichkeit eines Kurseinbruchs ab. Subjektive Eintrittswahrscheinlichkeit bedeutet, dass es sich hierbei um die kollektive Einschätzung der Marktteilnehmer handelt, denn die tatsächliche Eintrittswahrscheinlichkeit für einen Crash ist natürlich unbekannt. Vor dem Platzen der DotCom Blase war die subjektive Crash-Wahrscheinlichkeit des Marktes geringer als nach dem Ereignis.

Das Maß, mit dem im Options-Umfeld die Höhe der Crash-Gefahr ausgedrückt wird, ist die sog. Volatilität. Verläuft der Markt ruhig, sind Volatilität und somit auch die Crash-Gefahr gering. Geht es wild hoch und runter, dann sind Volatilität und Crash-Gefahr dagegen hoch.

Wer sein Depot vor Kurseinbrüchen schützen möchte zahlt mehr, wenn bereits erste graue Wolken am Himmel aufgezogen sind. Anfang Januar 2022 waren beispielweise ca. 70.000 Euro ausreichend, um ein Million-Depot 1 Jahr lang vor Kurseinbrüchen zu schützen. Anfang März, eine Woche nach Kriegsbeginn in der Ukraine, war die Versicherungsprämie dagegen auf ca. 13% angestiegen. Auf dem Höhepunkt der Corona-Krise lag der Preis für die entsprechende Put-Option bei ca. 25% des zu versichernden Kapitals, während der globalen Finanzkrise sogar bei ca. 30%.

Bei der Volatilität unterscheidet man die implizite Volatilität und die historische Volatilität. Die historische Volatilität stellt in der Vergangenheit beobachtete Kursschwankungen dar. Die implizite Volatilität drückt dagegen die für die Zukunft erwarteten Kursschwankungen aus. Für die Bepreisung einer Put-Option wird die in die Zukunft gerichtete implizite Volatilität benötigt. Sie ist die entscheidende Zutat in der Black-Scholes Formel. Ein wichtiger Index in diesem Zusammenhang ist der Volatility Index (VIX), welcher die implizite S&P 500-Volatilität über einen Zeitraum von 30 Tagen angibt. In Krisenzeiten schlägt der VIX nach oben aus, eine Versicherung vor Kurseinbrüchen ist dann dementsprechend teuer.

>Kernaussage Nr. 3: der Preis einer Put-Option hängt von der Volatilität des Marktes ab

Eine weitere wichtige Zutat für den Preis unserer Put-Option ist das Sicherheitsniveau. Soll der Put jegliches Risiko herausnehmen, oder besteht die Bereitschaft einen Teil des Verlustes selbst zu tragen, ähnlich einem Selbstbehalt einer Versicherung? In der Optionswelt spricht man hier vom Basispreis. Das ist das Preisniveau, ab dem der Schutz durch die Option greift. Liegt der DAX heute bei 14.000 Punkten, und liegt der Basispreis einer Put-Option auf den DAX z.B. bei 13.500, dann zahlt der Anleger die ersten 500 Punkte Kurs-Verlust aus eigener Tasche. Fällt der Markt aber anschließend unter den Basispreis, dann werden alle weiteren Verluste durch die Put-Option ausgeglichen. Der Käufer der Option ist somit gegen Kurseinbrüche unterhalb von 13.500 Punkten immunisiert.

Je höher das Sicherheitsniveau, desto höher der Preis der Option, das leuchtet ein. Wer möchte nicht gerne gegen sämtliche Risiken abgesichert sein? Die folgende Grafik veranschaulicht den Zusammenhang zwischen Schutzniveau / Basispreis und Options-Prämie für verschieden hohe Volatilitätsniveaus:

Wer von Angang an abgesichert sein möchte (100%), der muss zu normalen Zeiten (Volatilität 15% – 20%, blaue und orange Linien) ca. 60.000 bis 80.000 Euro Prämie zahlen, um ein Jahr vollständig vor Kurseinbrüchen geschützt zu sein. Man erkennt an dieser Stelle gut den Zusammenhang zwischen erwarteter Rendite des Aktienmarkts (ca. 7% = 70.000 Euro bei 1 Million Depotvolumen) und Risiko. Wer jegliches Risiko herausnimmt, erhält unterm Strich nur noch den risikolosen Zins, d.h. erwartete Rendite abzüglich der Optionsprämie, also nichts. Andernfalls wären die Märkte nicht fair bepreist.

Wer alternativ dazu bereit ist die ersten 10% Verlust selbst zu tragen (Sicherheitsniveau = 90%), der bezahlt für den einjährigen Versicherungsschutz bei 15% Volatilität (blaue Linie) nur noch 25.000 Euro (statt 60.000 Euro bei 100% Sicherheitsniveau) pro Million Depotvolumen.

>Kernaussage Nr. 4: der Preis einer Put-Option hängt neben der Volatilität auch vom gewünschten Sicherheitsniveau (Basispreis) ab

Was nicht passt wird passend gemacht

Aber wie wollen wir die für die Bepreisung wichtigste Zutat, die implizite Volatilität, für Zeiten ermittelt, zu denen es noch gar kein Optionspreismodell bzw. Optionen gab? Ohne zu wissen was eine Option in der Vergangenheit gekostet hätte, ist eine historische Simulation der hier vorgestellten Strategie gar nicht möglich. Wir müssen also einen Weg finden die implizite Volatilität der Vergangenheit zu rekonstruieren. Die Lösung basiert auf der historischen Volatilität.

Mit Hilfe täglicher Marktdaten des S&P 500 ist es möglich Veränderung der Volatilität relativ schnell zu erkennen. Es ist daher denkbar, die benötigte implizite Volatilität, welche ebenfalls schnell auf sich verändernde Rahmenbedingungen reagiert, mittels einer historischen Volatilität basierend auf Tageskursen anzunähern. Um das Ergebnis weiter zu verfeinern, habe ich zwei historische Volatilitäten berechnet, und anschließend das Maximum als Schätzer für die implizite Volatilität gewählt. Zunächst berechne ich die historische Volatilität auf Basis der vergangenen 250 Handelstage (1 Jahr), und habe so eine flexible, aber auch repräsentative Datengrundlage. Zusätzlich ergänze ich diese 1-jährige historische Volatilität um eine 3-monatige historische Volatilität. Diese basiert auf weniger Datenpunkten, reagiert dafür aber deutlich schneller auf Veränderungen. Dadurch, dass dieses Modell jeweils das Maximum der beiden Ergebnisse berücksichtigt, reagiert unser Schätzwert schnell auf Krisen. Sobald sich die kurzfristige Volatilität wieder beruhigt, steigt die langfristige Volatilität an, und wir wählen diese als neuen Maximalwert. Dadurch wird ein in der Praxis beobachteter „Nachhalleffekt“ bewahrt. Denn der Markt braucht nach einem Schockevent mehr Zeit um sich „im Inneren“ wieder zu stabilisieren, als die reine Kursentwicklung vermuten lässt.

Vergleicht man die so geschätzte implizite Volatilität mit dem VIX ab 1990, d.h. mit echten Marktdaten, dann ergibt sich folgendes Bild:

Eine Anmerkung zu der Grafik: da der VIX sich auf Optionen mit einer Laufzeit von 1 Monat bezieht, habe ich hier die kurze Volatilität dementsprechend über 21 Handelstage bestimmt.

Die Annäherung durch die historische Volatilität ist nicht perfekt, aber man kann damit realitätsnah arbeiten. Im Sinne einer konservativen Vorgehensweise empfiehlt es sich aber einen Puffer in Form eines Aufschlags auf die geschätzte Volatilität zu berücksichtigen.

Ein weiteres Detail, welches aufgrund seiner Bedeutsamkeit kurz erwähnt werden muss, ist der Volatilitäts-Smile. Das Thema ist kompliziert, aber die Options-Spezialisten unter den Lesern wären sicher sehr enttäuscht, wenn ich nicht kurz darauf eingehe. Denn die oben geschätzte Volatilität ist die Volatilität für Optionen am Geld. Tatsächlich steigt die implizite Volatilität je weiter die Option aus dem Geld ist (d.h. je geringer das Sicherheitsniveau der Crash-Versicherung ist). Würde man diesen Aspekt nicht berücksichtigen, dann würde die Höhe der Versicherungsprämie unterschätzt werden, so dass die Ergebnisse der Strategie ins positive verzerrt wären. Auch der Volatilitäts-Smile ist im Zeitablauf dynamisch. Man sieht, für eine absolut perfekt Analyse benötigt man umfangreiche Marktdaten von höchster Qualität. Sind diese nicht verfügbar, kann man mit einem gut begründeten Modell vorsichtig operieren. Ich habe daher den Volatilitäts-Smile aus Optionspreisen während des Ukraine-Kriegs entnommen, und halte diesen über den gesamten Zeitraum der historischen Analyse konstant.

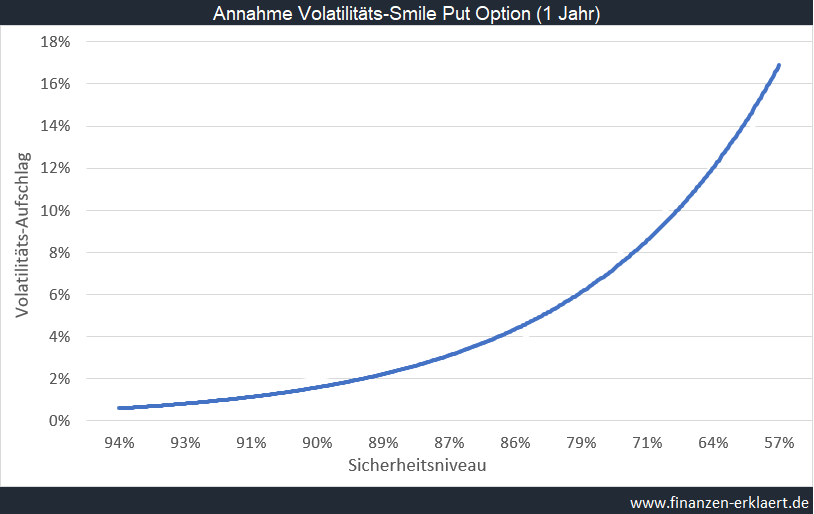
Eigentlich kann man hier gar nicht von einem Smile sprechen, denn hier sieht man nur die Put-Seite, nicht die Call Seite, welche wir für die hier betrachtete Strategie auch nicht benötigen.

Wer an dieser Stelle nur noch Bahnhof versteht, kann jetzt aufatmen. Es ist zum Thema Optionsbewertung genug gesagt. Ich habe ein paar vereinfachende Abkürzungen genommen und versucht mich auf das Wesentliche zu beschränken. Im ersten Schritt ging es darum das komplexe Thema verständlich rüberzubringen.

Durch den Kauf einer Put Option steigt die sichere Entnahmerate

Mit den historischen Volatilitätsdaten ist es möglich den historischen Kaufpreis einer Put-Option zu bestimmen. Dieser muss zu Beginn der Entnahmephase gezahlt werden, um sich gegen einen unmittelbaren Crash am Aktienmarkt (bzw. das Renditereihenfolgerisiko) zu versichern. Ein Jahr später, wenn die Laufzeit der Option abgelaufen ist, wird die Marktentwicklung mit dem Sicherheitsniveau verglichen. Ist der Markt nach Kauf der Option unter das Sicherheitsniveau gefallen, dann erhält der Käufer der Option eine Ausgleichszahlung.

Beispiel: Eine Option versichert ein Depotvolumen von einer Million Euro. Das Sicherheitsniveau liegt bei 80%, der Kaufpreis bei ca. 20.000 Euro. Ein Jahr später ist der Markt um 30% gefallen. Die ersten 20% Verlust trägt der Käufer aufgrund des Sicherheitsniveaus von 80% selbst, die verbleibenden 10% sind durch die Option abgedeckt, werden erstattet. Der Käufer erhält am Ende der Laufzeit dementsprechend eine Ausgleichszahlung von 1 Million x 10% = 100.000 Euro. Es verbleibt nach Abzug der Kaufprämie ein Netto-Ertrag von 80.000 Euro.

Durch die Ausgleichszahlung wird das für die Entnahmephase besonders wesentliche Renditereihenfolgerisiko spürbar reduziert. Schwere Kurseinbrüche verlieren ihren Schrecken. Im Gegenzug muss für diesen Schutz ein Teil des Kapitals für den Kauf der Put-Option aufgewendet werden. Kommt es nicht zum Crash, dann verfällt die Option wertlos und die Kaufprämie ist verloren. In diesem Fall befinden wir uns aber auf einem Rendite-Pfad, der eine höhere Entnahme zulässt, so dass der Verlust der Kaufprämie nicht weiter stören sollte.

Nachdem die Vorgehensweise bei der Analyse sowie die praktische Umsetzung der Strategie dargestellt wurden, werfen wir nun endlich einen Blick auf die Ergebnisse der historischen Simulation:

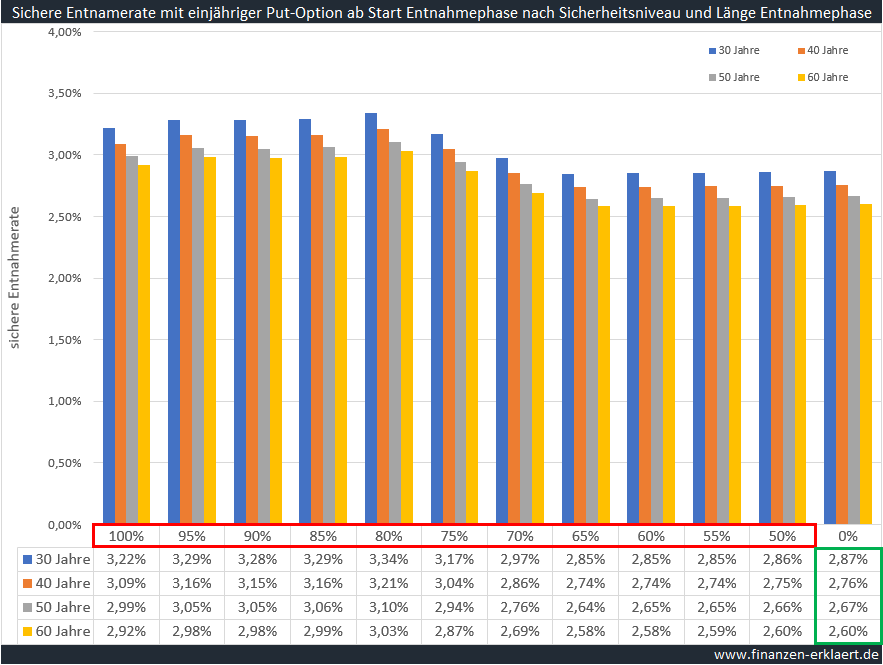
Die Grafik beinhaltet eine Vielzahl an Informationen. Ich habe sämtliche Berechnungen für Entnahmephasen von 30, 40, 50 und 60 Jahren Dauer durchgeführt, hier dargestellt durch die verschieden farbigen Balken. Die Höhe der Balken stellt die sichere Entnahmerate dar. Die Gruppe bestehend aus vier Balken ganz rechts stellt die sichere Entnahmerate ohne Optionsstrategie dar. Die exakten Werte befinden sich in der Wertetabelle darunter (grüner Rahmen). Ganz unten die berühmten 2,6% für den 60-jährigen Entnahmezeitraum.

Alle weiteren 4er-Gruppen zeigen die sichere Entnahmerate mit Optionsstrategie bei unterschiedlichen Sicherheitsniveaus (roter Rahmen). Ganz links die Variante Sicherheitsniveau = 100%. Hier wird durch die Option jegliches Kursrisiko entfernt, dementsprechend ist auch eine üppige Optionsprämie fällig. Trotzdem liegt die sichere Entnahmerate deutlich über dem Niveau ohne Optionsstrategie.

Wer bereit ist geringe Verluste zu akzeptieren, der kann die sichere Entnahmerate sogar noch etwas steigern. Denn die Optionsprämie ist hier geringer, während wir weiterhin vor sehr adversen Szenarien geschützt sind. Und genau diese besonders adversen Szenarien prägen die sichere Entnahmerate, weshalb es sinnvoll ist, diesen Trade-off aus Risiko und geringerer Optionsprämie zu akzeptieren. Ein Sicherheitsniveau von 80% erscheint als Optimum, darunter verliert die Optionsstrategie deutlich an Wirksamkeit, unterhalb von 70% leistet die Optionsstrategie sogar einen negativen Beitrag.

Fazit

Eine spannende Entnahmestrategie, die in dieser Form meiner Kenntnis nach bisher noch nicht untersucht wurde. Der Grund liegt sicherlich auch darin, dass die benötigten Daten für absolut präzise Berechnung nicht leicht bzw. gar nicht verfügbar sind. Um die Robustheit der Strategie zu überprüfen habe ich aus diesem Grund weitere Berechnungen durchgeführt, bei denen ich die geschätzte implizite Volatilität zusätzlich um den Faktor 1,5 skaliert habe, was einen enormen Aufschlag darstellt. Selbst dann liefert die Strategie konsistent positive Ergebnisse. Wer die eigene Entnahmestrategie auf sehr adverse Marktentwicklungen wie den großen Crash während der 30er Jahre (-85% über 3 Jahre) kalibriert, der kann mit der Put-Strategie die Entnahmen deutlich steigern. Denn für genau solche extremen Ereignisse stellen Optionen einen günstigen Versicherungsschutz dar. Diese faszinierende Entnahmestrategie möchte ich gerne in Zukunft noch detaillierter untersuchen. Offene Fragen sind beispielsweise, ob es sinnvoll ist mehrere Optionen mit verschiedenen Laufzeiten zu kombinieren, oder in den ersten Jahren der Entnahmephase weitere Optionen zu kaufen, falls sich die Märkte währenddessen positiv entwickeln. Ab 1990 sollten sogar Tests mit qualitativ hochwertigen Daten (VIX) möglich sein. Doch für heute genug.