Entnahmestrategien optimieren: Wieviel Rendite darf eine Reduktion der Volatilität maximal kosten?

Das Thema Renditereihenfolgerisiko wurde in einem früheren Artikel schon einmal intensiv beleuchtet. Gäbe es am Aktienmarkt beispielsweise in jedem Jahr exakt 7% Rendite, dann könnte man in jedem Jahr risikolos über 7% des Kapitals verfügen, ohne dadurch den Erhalt des Kapitalstocks zu gefährden. In der Realität schwanken die Renditen jedoch stark. Statt einer konstanten Durchschnittsrendite streuen die einzelnen beobachteten jährlichen Renditen um den langfristigen Durchschnitt. Kommt es zu Beginn der Entnahmephase zu einem Crash, wird das Portfolio durch Entnahmen überproportional stark entspart. In der Konsequenz liegt in diesen Fällen die maximal zulässige Entnahmerate deutlich unter der langfristigen Durchschnittsrendite. Das Risiko stark negativer Renditen am Anfang nennt man Renditereihenfolgerisiko, davor gilt es sich durch eine konservative Finanzplanung zu schützen.

In der Volatilität liegt die Ursache für das Renditereihenfolgerisiko

Die einzige Möglichkeit die Volatilität renditeschonend zu reduzieren ist durch Nutzung von Diversifikationseffekten. Zunächst auf der Ebene der Assetklasse, indem z.B. bei Aktien nicht in Einzeltitel, sondern in ein gut diversifiziertes Weltportfolio investiert wird. Darüber hinaus im nächsten Schritt auch zwischen Assetklassen, z.B. durch Aufnahme von Anleihen oder Rohstoffen in das Portfolio. Jedoch lässt sich in diesem Fall ein Renditeverlust auf Portfolioebene durch Ausnutzung von Diversifikationseffekten nur abmildern, aber nicht vollständig verhindern. Dafür ist der relative Renditenachteil der alternativen Asset-Klassen einfach zu hoch. Die langfristige Rendite von Gold liegt beispielsweise ca. 6% unter der eines gut diversifizierten Aktienportfolios, bei Staatsanleihen beträgt der Abschlag ca. 4,5%. Diese enormen Rendite-Unterschiede können im Allgemeinen nicht durch Diversifikationseffekte kompensiert werden, so dass Portfolios mit geringerer Volatilität auch eine geringere erwartete Rendite aufweisen.

In diesem Artikel werfen wir einen detaillierten Blick auf die Volatilität als Verursacher und Treiber des Renditereihenfolgerisikos. Es geht dabei nicht nur um die Frage wie unterschiedliche Volatilitätsniveaus auf die sichere Entnahmerate wirken. Wir werden uns insbesondere auch ansehen, auf wieviel Renditeerwartung man maximal verzichten darf, um die Volatilität effektiv zu reduzieren. Dass eine reduzierte Volatilität einen positiven Effekt auf die Entnahmemöglichkeiten hat, ist nachvollziehbar. Will man aber die Volatilität reduzieren, dann kostet dies regelmäßig auch erwartete Rendite. Keine Volatilität bedeutet kein Risiko, und kein Risiko bedeutet derzeit keine erwartete Rendite. Wer jegliche Volatilität vermeiden will, für den bleibt nur das Tagesgeld zum risikolosen Zins. Der Zusammenhang zwischen Risiko und Renditeerwartung wird im Allgemeinen durch die sog. Kapitalmarktlinie beschrieben.

Auf nach Monte-Carlo!

Es stellt sich daher die Frage nach dem Break-Even, d.h. nach dem Punkt, ab dem eine Reduktion der Volatilität auf Kosten der erwarteten Rendite für die Entnahmen schädlich ist. Um diesen Zusammenhang genau untersuchen zu können bedarf es Renditesequenzen aus der Retorte, d.h. es ist der Einsatz einer zufallsgetriebenen Monte-Carlo Simulation erforderlich.

Normalerweise bevorzuge ich eine historische Simulation, denn die Aktienmärkte lassen sich meiner Meinung nach nicht ausreichend gut durch einen mathematischen Zufallsprozess mit begrenzten Parametern beschreiben. Im Rahmen einer Monte-Carlo Simulation wird die Anzahl der Variablen willkürlich begrenzt. Die historischen Daten funktionieren dagegen wie eine Black-Box. Die darin enthaltenen Werten beinhalten eine unüberschaubare Menge an Variablen, bis hin zum Einfluss von Fake-News, Gier und Angst auf das menschliche Verhalten.

Die Monte-Carlo Simulation ist insofern ehrlich, als sie die ihr zugrunde liegenden Parameter des Zufallsprozesses immer offenlegt. D.h. wie hoch soll beispielsweise die erwartete Rendite sein? So wie in der Vergangenheit bei durchschnittlich ca. 7%, oder vielleicht nur 5% oder 3%? Und was ist mit der Höhe der Volatilität? Hier kommt es schnell zu einem unlösbaren Dilemma was die korrekte Einstellung des Zufallsgenerators betrifft. Die Verwendung historischer Daten mit all den darin enthaltenen verschiedenen Epochen und Ereignissen verschafft dem Anleger dagegen nicht nur Orientierung, sondern liefert auch eine Antwort auf die Frage nach der Ausprägung des maximalen Stresses.

Abschließend sollte bei der Verwendung eines Zufallsgenerators bedacht werden, dass bei unendlicher Wiederholung nahezu jedes beliebige Ereignis auftreten wird. Man muss den Generator nur oft genug einsetzen, irgendwann produziert dieser auch eine Rendite-Sequenz bei der im ersten Jahr 99,9% des Vermögens vernichtet werden.

In diesem Fall mache ich aber eine Ausnahme. Denn das historische Datenmaterial ist nicht lang und „sauber“ genug, um präzise Untersuchungen über das Zusammenspiel von Rendite und Volatilität präzise zu erlauben. Alle folgenden Berechnungen basieren daher auf jeweils 10.000 Simulationsläufen einer von mir eingestellten Monte-Carlo Simulation. Konkret habe ich 10.000 monatliche Renditesequenzen für einen 30-jährigen Zeitraum berechnet, das sind 12 x 30 x 10.000 = 3,6 Millionen zufällige Monatsrenditen. Den zugrunde liegenden stochastischen Prozess habe ich mit einer erwarteten Rendite von 7% und einer Volatilität von 17,5% ausgestattet. Dies entspricht in etwa den langfristigen historischen Durchschnittswerten des Aktienmarkts. Für jede einzelne dieser 10.000 zufällig generierten Renditesequenzen habe ich anschließend die sichere Entnahmerate mit Kapitalerhalt berechnet. Die folgende Grafik zeigt die Ergebnisse sortiert von minimal (links) bis maximal (rechts):

Ohne Volatilität läge die Entnahmerate garantiert bei konstant 7%, das zeigt uns die rote Linie. Mit Einbezug der Volatilität beginnen die Ergebnisse zu variieren (dunkelblau). In etwas mehr als 55% der Fälle liegt die sichere Entnahmerate unterhalb des Wertes ohne Volatilität. Das ist auf den ersten Blick erstaunlich, und geht auf den Einfluss der Volatilität zurück. (Zur Information: Das arithmetische Mittel über alle beobachteten Entnahmeraten (nicht in der Grafik dargestellt) entspricht dagegen exakt der durchschnittlichen Rendite, was auf eine schiefe Verteilung der Entnahmeraten deutet). Des Weiteren ist ein Teil der gemessenen Entnahmeraten negativ, wodurch die eingangs beschriebene Schwäche hinsichtlich der durch die Monte-Carlo Simulation produzierten Extremwerte noch einmal unterstrichen wird.

Doch absolute Niveaus interessieren uns heute nicht, so dass wir über diesen Nachteil unserer Simulation hinwegsehen können. Stattdessen interessiert uns der relative Vergleich. Die folgende Grafik zeigt beispielsweise was passiert, wenn man die erwartete Rendite bei 7% belässt, die Volatilität aber variiert:

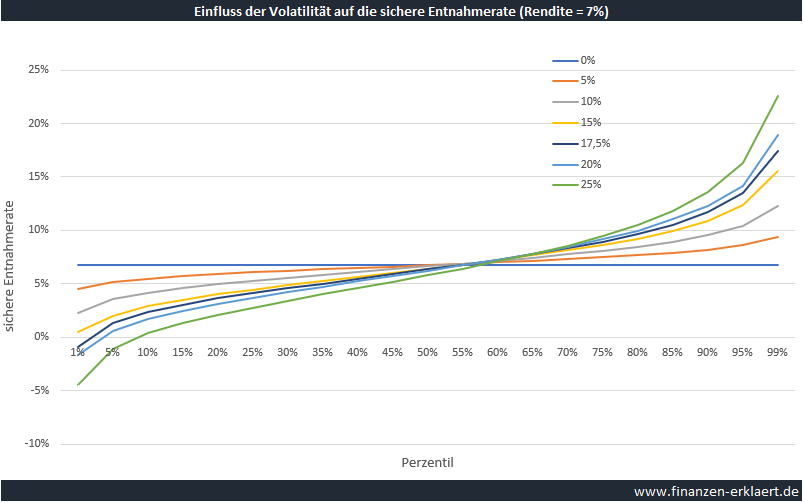
Man erkennt deutlich, wie sich der Fächer der Möglichkeiten mit zunehmender Volatilität weiter öffnet. Der Schnittpunkt mit der Geraden der Durchschnittsrendite wandert mit zunehmender Volatilität immer weiter nach rechts. Außerdem wird klar, dass Volatilität neben Risiken auch Chancen generiert, denn ein wesentlicher Teil der beobachteten Entnahmeraten liegt oberhalb der erwarteten Rendite.

Und wie ändert sich das Bild, wenn die Volatilität konstant bei 17,5% gehalten wird, die erwartete Rendite jedoch in 1%-Schritten abnimmt? Werfen wir einen Blick auf die folgende Grafik:

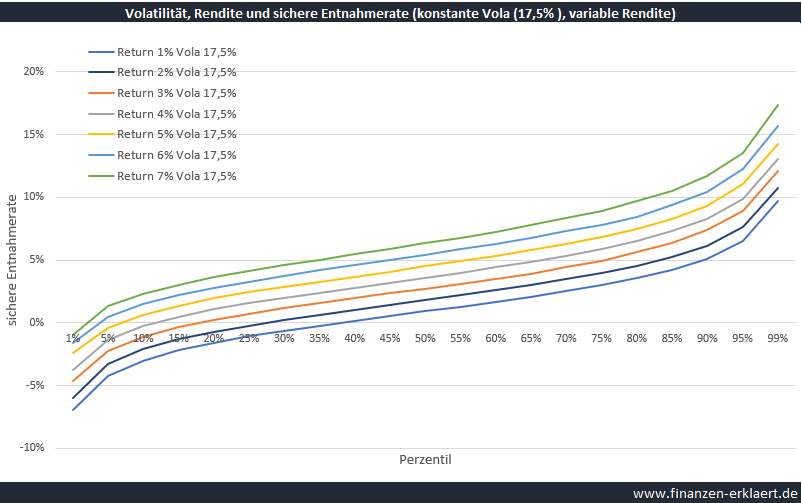
Bei konstanter Volatilität (hier: 17,5%) führt eine Veränderung der erwarteten Rendite zu einer Parallelverschiebung der im Zufallsexperiment beobachteten Entnahmeraten.

Wieviel Rendite darf die Reduktion der Volatilität maximal kosten?

Spannend sind an dieser Stelle verschiedene Kombinationen aus Volatilität und Rendite. Was passiert beispielsweise, wenn man die Volatilität reduziert, dafür im Gegenzug aber 1% erwartete Rendite hergeben muss? Die nachfolgende Grafik erlaubt es uns ein besseres Gefühl für diese Zusammenhänge zu entwickeln:

Die dunkelblaue Linie stellt den Ausgangspunkt dar. Hier liegt die Rendite bei 7% und die Volatilität bei 17,5%. Bei allen anderen Linien beträgt die Rendite nur noch 6%, und die Volatilität variiert. Die grüne Linie steht beispielsweise für die Kombination Rendite = 6% und Volatilität = 15%. Die Interpretation ist wie folgt: Um die Volatilität von ursprünglich 17,5% auf 15% zu verringern war es erforderlich die erwartete Rendite von 7% auf 6% zu reduzieren. In den meisten Szenarien produziert die blaue Rendite-Risiko Kombination höhere Entnahmeraten. Ganz links, in den niedrigen Perzentilen, macht sich die reduzierte Volatilität dann aber positiv bemerkbar: Die grüne Linie liegt minimal oberhalb der blauen Linie, d.h. im Extremfall, wenn es an den Märkten richtig kracht, kann eine geringfügige Reduktion der Volatilität bereits Vorteile generieren.

Gelingt es sogar die Volatilität für 1%-Punkt Verlust an erwarteter Rendite auf 12,5% oder noch niedriger zu senken, dann erfährt man schon in etwas mehr als 10% der Fälle einen positiven Effekt. Da bei der risikoorientierten Finanzplanung insbesondere die niedrigen Perzentile (<10%), also die Stressszenarien, im Fokus stehen, liefert die Reduktion der Volatilität einen echten Mehrwert. Voraussetzung ist, dass es uns gelingt die Volatilität im Vergleich zur erwarteten Rendite überproportional stark zu reduzieren. Ein Versprechen das viele Vermögensverwalter gerne geben.

Aber was, wenn die Reduktion der Volatilität einen höheren Preis einfordert? Wenn beispielsweise die erwartete Rendite von 7% auf nur noch 5% reduziert werden muss, um eine Reduktion der Volatilität zu erreichen? Mit einem klassischen 60% Aktien 40% Anleihen Portfolio konnte man in der Vergangenheit die Volatilität auf 10,71% reduzieren, durfte dafür aber auch nur eine geringere Rendite von 5,47% erwarten. Ob dies im aktuell niedrigen Zinsniveau auch gilt, ist mehr als fragwürdig, aber werfen wir trotzdem einen Blick auf die folgende Grafik:

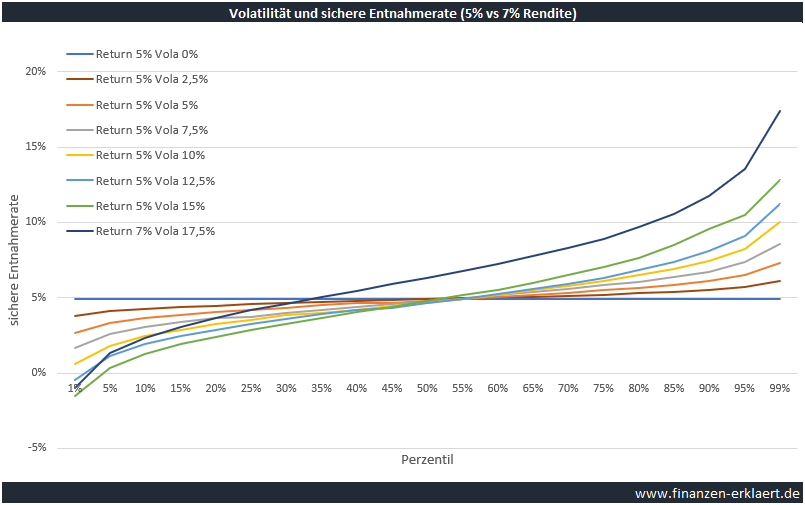
Anhand der Grafik wird sichtbar, dass bei 2%-Punkten weniger Rendite die Volatilität um mindestens 5%-Punkte zurückgehen muss, andernfalls handelt es sich um ein schlechtes Geschäft. Gelingt eine Reduktion auf ein Niveau von 10% oder weniger, dann liegen die entsprechenden Linien auf der linken Seite oberhalb der dunkelblauen Vergleichslinie (7% Rendite + 17,5% Volatilität), es handelt sich also um einen im Rahmen der Entnahmen sinnvollen Trade-Off.

Viel wahrscheinlicher ist jedoch, dass das klassische 60% Aktien / 40% Anleihen Portfolio im gegenwärtigen Niedrigzinsumfeld eine deutlich geringere Rendite aufweisen wird. Und der Vermögensverwalter will auch ein Stück vom Kuchen. Die folgende Grafik zeigt was passiert, wenn die erwartete Rendite von 7% auf nur noch 3% fällt:

Viele der alternativen Verläufe liegen jetzt deutlich unterhalb der dunkelblauen Referenzlinie. Die Portfolio-Volatilität muss durch Diversifikation verlässlich unterhalb von 10% fallen, besser sogar unter 7,5%, damit in Stresssituationen höhere Entnahmen möglich sind als mit einer 100%igen Aktienquote.

Fazit

Dieser Artikel stellt den Zusammenhang von Rendite, Rendite-Volatilität und sicherer Entnahmerate dar. Um die dafür benötigten Daten in entsprechender Qualität zu erzeugen haben wir uns ausnahmsweise der Monte-Carlo Simulation bedient. Eine Schwäche der Monte-Carlo Simulation ist die Erzeugung von unrealistischen Extremwerten, d.h. es kommt zufallsbedingt zu sogenannten Ausreißern, die das Ergebnis verzerren. Aus diesem Grund wurden in sämtlichen Grafiken auch nur die Werte des 1%- bis 99%-Perzentils abgebildet. Das beeinträchtigt aber nicht die Möglichkeit des Vergleichs zwischen verschiedenen Szenarien der Monte-Carlo Simulation, d.h. die Ergebnis-Differenzen können durchaus als stabil betrachtet werden.

Die Analyse zeigt klar auf, dass eine Reduktion der Volatilität während der Entnahmephase grundsätzlich vorteilhaft ist. Jedoch darf die Reduktion der Volatilität die benötigte Rendite nicht zu stark aufzehren. Ansonsten kippt das Bild, so dass die Entnahmeraten trotz geringerer Volatilität sinken. Besonders schädlich sind hier die Kosten einer Vermögensverwaltung, da dadurch die Rendite ohne jeglichen Effekte auf die Volatilität reduziert wird (Parallelverschiebung der Kurve im Diagramm nach unten).

Wer hingegen chancenorientiert ist, weil die essenziellen Positionen des Lebensunterhalts bereits durch alternative Geldquellen abgedeckt sind, der sollte überlegt vorgehen. Denn die vorliegende Analyse zeigt ebenfalls klar auf, dass mit Volatilität auch eine Chancen für höhere Entnahmen verbunden ist, die sich bei einem positiven Marktverlauf durch progressives Entnehmen abschöpfen ließe.

Abschließend muss noch erwähnt werden, dass wir hier die komplexe Realität stark vereinfacht haben. Denn niemand kann im Vorhinein wissen, welches Chance-Risiko Profil eine bestimmte Asset-Kombination aufweisen wird, d.h. welche präzisen Auswirkungen beispielsweise die Beimischung von 40% Staatsanleihen auf die Portfolio-Rendite und -Volatilität haben wird. Die exakten Daten sind immer erst im Nachhinein bekannt. Mit dem Blick nach vorne gerichtet bleibt nur die Hoffnung. Und je mehr Variablen (d.h. Assets und deren Korrelationen untereinander) das Bild beeinflussen, desto weniger kann ein Modell als zuverlässige Prognose für die Zukunft dienen. Für mich persönlich ein guter Grund die Komplexität und damit verbunden auch die Unsicherheit bei der Entnahmeplanung möglichst gering zu halten.