Vorsicht vor der 4% Regel

Mit diesem Artikel starte ich eine Serie über Entnahmestrategien. Das Thema persönliche Finanzen lässt sich grob in 2 große Bereiche aufteilen: erstens in „Vermögen aufbauen“ und zweitens in „von Vermögen leben“.

„Vermögen aufbauen“ ist für die meisten Menschen von Interesse. Viele legen regelmäßig etwas Geld beiseite, um davon später irgendwann mal irgendwas zu kaufen, oder um fürs Alter abgesichert zu sein.

Wer Geld für die Altersvorsorge spart, muss sich irgendwann fragen, wie er die Ersparnisse im Alter verbrauchen will. Und genau darum geht es in dieser Artikelserie. Konkret geht es um verschiedene Entnahmestrategien. Darunter versteht man Methoden mit denen man die eigenen Ersparnisse möglichst optimal verbraucht. Optimal bedeutet in dem Zusammenhang, dass die Entnahmebeträge möglichst hoch und im Zeitablauf konstant sind. Außerdem soll gleichzeitig das Risiko eines vorzeitigen, vollständigen Vermögensverbrauchs reduziert werden.

Die einfachste aller Entnahmestrategien sieht wie folgt aus: man lagert seine Ersparnisse in Form von Guthaben auf dem Girokonto und nimmt sich davon jedes Jahr einen gleichen Anteil. Wer z.B. 400.000 Euro besitzt kann über 40 Jahre jeweils 10.000 Euro (= 2,5%) pro Jahr entnehmen, oder über 20 Jahre 20.000 Euro (= 5%) pro Jahr usw. Diese Strategie erfüllt schon mal das Kriterium der konstanten Beträge. Wer sich aber bei der Länge des Zeitraums verplant, der steht irgendwann mittellos da. Als Unterstützung für die eigene Rente wären 40 Jahre daher eher zu empfehlen als 20 Jahre. Aber je länger die Entnahmeperiode, desto geringer der jährliche Entnahmebetrag. Und die Inflation wird auch nicht berücksichtigt, der jährliche Entnahmebetrag ist also im Zeitablauf real immer weniger Wert. Die Kaufkraft schwindet dahin.

Daher stellt sich die Frage ob es eventuell einen Weg gibt über einen Zeitraum von 40 Jahren mehr als nur 2,5% jährlich zu entnehmen. Und was ist mit der Inflation – die regelmäßigen Entnahmen müssten doch eigentlich jährlich steigen um die Kaufkraft zu erhalten? Mit diesen Problemen befassen sich die Entnahmestrategien.

Die wohl populärste Entnahmestrategie ist die 4% Regel

Wer sich mit dem Thema Entnahmestrategien beschäftigt, stößt recht schnell auf die 4% Regel. Die 4% Regel geht auf die Trinity Study aus dem Jahr 1998 zurück. Sie besagt, dass man einem diversifizierten Aktien-Portfolio über einen Zeitraum von 30 Jahren in jedem Jahr 4% des Anfangswertes entnehmen kann, bei gleichzeitig sehr geringem Risiko vorzeitig das Vermögen vollständig zu verbrauchen. Das ist schon mal ein Vorteil, denn in der Bargeldvariante oben wären über einen Zeitraum von 30 Jahren in jedem Jahr nur 3,33% pro Jahr möglich gewesen.

Darüber hinaus zeigt die Studie: wird der Entnahmebetrag jährlich um die Inflation angepasst, dann ist das Risiko eines vorzeitigen vollständigen Vermögens-Verbrauchs immer noch recht gering. Auch hier ein klarer Vorteil der 4% Regel.

Bitte beachte die letzten beiden Absätze sehr sorgfältig.

Denn dort steht „30 Jahre“ und nicht „für immer“. Und einer sehr geringen, aber nicht ausgeschlossenen Pleitegefahr.

In gefühlt mehr als 99% der Internetquellen zu diesem Thema liest man aber, dass die 4% Regel niemals versagt, und für jeden x-beliebig langen Zeitraum anwendbar ist. Dieses „Wissen“ wird dann ungeprüft weitergegeben und übernommen, so dass daraus heutzutage ein allgemeingültiges Gesetz entstanden ist, das kaum jemand mehr in Frage stellt.

Ganze Lebensentwürfe basieren auf dieser Regel. Man liest davon, dass man der 4% Regel entsprechend das 25-fache der eigenen jährlichen Ausgaben sparen muss, um anschließend für immer finanziell frei zu sein. Und eine jährliche Anpassung des Entnahmebetrags um die Inflation soll auch noch drin sein!

Wer aber vermeiden möchte, dass der eigene Seifenblasentraum auf Basis der 4%-Regel gleich zu platzen droht, der sollte am besten an dieser Stelle aufhören weiterzulesen.

Die Trinity Studie lässt viele Fragen unbeantwortet

Ich kann nur jedem empfehlen die eigene Zukunft nicht naiv auf solch essentielle Annahmen zu basieren. Stattdessen sollte man diese gründlich prüfen bevor man sein eigenes Leben danach ausrichtet. Und genau dies werden wir jetzt tun! Im ersten Schritt habe ich die Trinity Study selbst nachgestellt, und basierend auf Daten des S&P 500 von 1900 – 2019 für verschieden lange Zeiträume überprüft, welche Entnahmerate wirklich funktioniert hätte. Hierbei habe ich alles möglichst identisch zur Trinity Studie gehalten.

In zukünftigen Beiträgen werde ich dann die Untersuchung um einige Aspekte, die für die do-it-yourself Rentenversicherung gemäß der 4% Regel von hoher praktischer Relevanz sind, ergänzen. Folgenden Aspekte werde ich genauer unter die Lupe nehmen:

• Die laufenden Kosten eines Wertpapierdepots: auch wenn es heute möglich ist über ETFs relativ günstig investiert zu sein, so gibt es die Geldanlage nicht zum Nulltarif. Und ab und zu sind auch noch Transaktionskosten durch Verkäufe fällig. Wir schauen uns deshalb an wie sich das TER auf die Entnahmerate auswirkt.
• Relevante Zeitperiode: die Trinity Study und auch meine eigenen Berechnungen berücksichtigen beide die Weltwirtschaftskrise im Jahr 1929. Das hat einen erheblichen Einfluss auf die sichere Entnahmerate. Denn diese ist dann automatisch so eingestellt, dass auch die größte Krise aller Zeiten überstanden werden kann. Doch haben wir wirklich nichts aus den Fehlern der Vergangenheit gelernt? Oder können wir solch heftige Krisen vielleicht für die Zukunft ausschließen? Ich denke ja, weshalb wir hier eine zweite Rechnung für die neuere Zeit ab 1975 aufmachen werden.
• Inflation: Die Trinity Study berücksichtigt u.a. auch die Inflation indem die Entnahmerate regelmäßig nach oben angepasst wird. Dadurch bleibt die Kaufkraft im Zeitablauf konstant. Die Studie geht dabei davon aus, dass die Inflation welche auf die Kaufkraft wirkt auch die gleiche ist, die die nominalen Renditen treibt. Dadurch hat man als Anleger einen impliziten Schutz, denn fallende Aktienkurse gehen oft (nicht immer) mit einem Rückgang der Inflation einher. Die Entnahmerate wird also in Zeiten fallender Kurse weniger stark nach oben angepasst. Für einen Investor der in den USA lebt und ausschließlich in US Titel investiert ist mag diese Sichtweise passend sein. Aber für einen US-Ausländer kann der Sachverhalt ganz anders sein. Denn die Inflation des Marktes in den ich investiert bin, muss nicht der Inflation des Landes in dem ich lebe entsprechen. Sind Investitionsland und Konsumland verschieden, dann funktioniert der implizite Schutz nicht mehr so gut, was zusätzliche Risiken birgt. Das hat wiederum Konsequenzen auf die Entnahmerate.
• Wechselkursschwankungen: viele Sparer in Deutschland investieren in Aktien und Indizes die in USD notieren und verzichten aus Kostengründen oder Überzeugung auf die Wechselkursabsicherung. Hier stellt sich also die Frage wie sich Wechselkursschwankungen auf die Entnahmerate auswirken? Ist es vielleicht sinnvoller sich gegen Wechselkursschwankungen abzusichern und dafür ein höheres TER zu akzeptieren?
• Steuern: Wer in Wertpapiere investiert, will damit eine Rendite erzielen. Und wer Rendite erzielt, gerät ins Visier des Fiskus. Es ist davon auszugehen, dass bei der regelmäßigen Entnahme auch Gewinne realisiert und damit Steuern gezahlt werden. Diese schmälern die effektive Nachsteuer-Entnahmerate. Welchen Puffer sollte man also für Steuern einplanen? Und wie lautet die um Steuern adjustierte sichere Entnahmerate?

Spätestens an dieser Stelle ist klar, dass ich mit dieser Menge an Fragen den Rahmen eines einzelnen Artikels sprengen würde. Daher werde ich diesem wichtigen Thema eine eigene Serie widmen. Heute geht es zunächst um die Grundlagen, d.h. um eine detaillierte Darstellung und Überprüfung der sicheren Entnahmerate wie diese auch die Trinity Studie ermittelt hat.

Die Wahrheit über die 4% Regel

Die Wahrscheinlichkeit innerhalb von 30 Jahren mit der 4% Regel zu scheitern beträgt 2,9%! Bäm! Da ist die Katze auch schon aus dem Sack heraus. Die 4% Regel ist über einen Zeitraum von 30 Jahren leider nicht sicher. Dabei habe ich unterstellt, dass der Entnahmebetrag jährlich um die Inflation angepasst wird, so wie es auch die meisten Quellen im Internet tun. Zu demselben Ergebnis kommt übrigens auch die Studie selbst. Niemals wurde behauptet, dass die 4% Regel zu 100% sicher ist. Doch dieses kleine aber wichtige Detail ist bei vielen Beiträgen zum Thema Entnahmestrategien scheinbar verloren gegangen.

Viele Anhänger der FiRe Bewegung planen sogar mit noch viel längeren Rentenzeiten als nur mit 30 Jahren. Wer z.B. mit 40 in Frührente geht, der sollte für die nächsten 50-60 Jahre gewappnet sein. Dem medizinischen Fortschritt sei Dank. Die folgende Grafik stellt die Fehlerwahrscheinlichkeit der 4% Regel in Abhängigkeit vom Entnahmezeitraum dar. Aus Spaß habe ich mir erlaubt dies für Zeiträume bis zu 100 Jahren zu ermitteln:

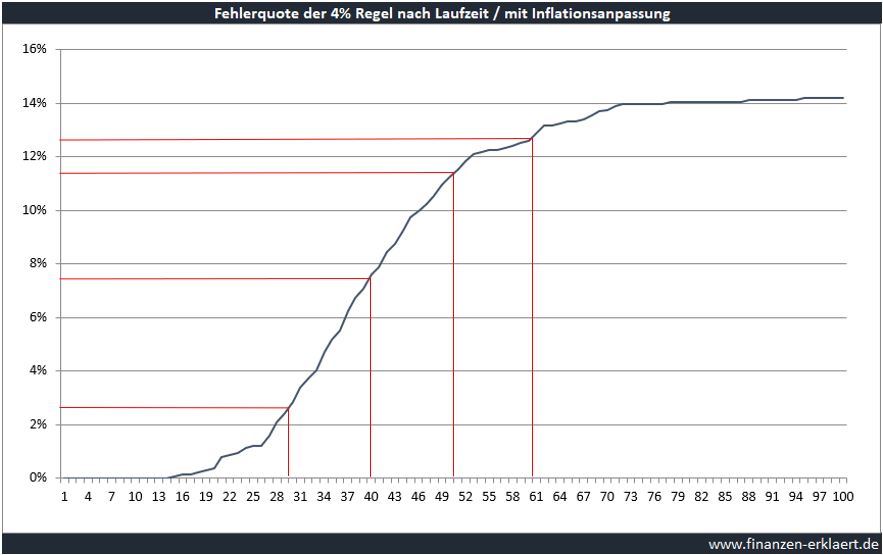
So richtig sicher scheint die 4% Regel nur für Zeiträume bis ca. 15 Jahre zu sein. Anschließend steigt die Fehlerwahrscheinlichkeit rapide an, um sich dann ab ca. 70 Jahren Entnahme bei grob 14% einzupendeln. 70 Jahre sind natürlich ein langer Zeitraum. Aber auch bei 40 Jahren ist die Fehlerwahrscheinlichkeit mit 7,6% schon recht hoch. Und für 50 Jahre steigt diese dann noch weiter auf 11,25% an. Das bedeutet, mehr als jeder 10. Anhänger der 4%-Regel wird während seines Ruhestands in Schwierigkeiten geraten.

Das wäre mir persönlich viel zu hoch!

So stelle ich mir die finanzielle Freiheit und meinen Lebensabend jedenfalls nicht vor. Ich möchte diese Zeit genießen und mir nicht die ganze Zeit Sorgen darüber machen ob das Geld am Ende vielleicht doch nicht reichen wird.

Aber auch wer bereit ist ein paar Prozentpunkte Fehlerquote zu akzeptieren, sollte nicht gleich entspannt sein. Denn unter den Anlegern die es am Ende schaffen werden sind garantiert auch noch mal einige dabei, bei denen es zwischendurch richtig knapp wurde. Angenommen das Kapital hat während einer Krise plötzlich stark an Wert verloren, obwohl noch viele Jahre davon zu leben wären. Das führt in dem Moment zu enormen Stress. Solche Erfahrungen will im hohen Alter wirklich niemand machen!

Ohne Inflationsanpassung sieht es schon besser aus

Wer dagegen darauf verzichtet den Entnahmebetrag der Inflation anzupassen, der hat deutlich bessere Chancen. Doch hierbei handelt es sich auf lange Sicht um Selbstbetrug. Denn auch mit geschicktem Verhalten kann man der Inflation auf Dauer nicht entkommen. Und die Kaufkraft schwindet, so dass real am Ende immer weniger übrigbleibt. Trotzdem hier kurz ein Chart, der zeigt wie sich diese Anpassung auf die Fehlerquote der 4% Regel auswirkt:

Der Unterschied ist für den 30-Jahres Zeitraum erstaunlich gering. Während die Fehlerwahrscheinlichkeit der 4%-Regel mit Inflationsanpassung über einen Zeitraum von 30 Jahren bei 2,87% liegt, beträgt diese ohne Inflationsanpassung immer noch 1,58%. Bei längeren Zeiträumen stellt sich dann aber ein signifikanter Unterschied ein, was mit dem Zinseszins-Effekt, angewandt auf die Inflation, zu tun hat.

Wie hoch ist denn nun die wahre, sichere Entnahmerate?

Sicherlich fragst Du Dich an dieser Stelle wie hoch die sichere Entnahmerate denn nun wirklich ist. Die gleiche Frage habe ich mir natürlich auch gestellt, und deshalb entsprechende Berechnungen angestellt. Dabei rechnen wir mit einer regelmäßigen Anpassung um die Inflation, denn wir möchten unsere Kaufkraft langfristig erhalten:

Wie man sieht liegt die sichere Entnahmerate für einen Zeitraum von 30 Jahren deutlich unterhalb von 3%. Dies liegt daran, dass die zugrunde liegende Zeitreihe die Weltwirtschaftskrise, die schwerste Krise aller Zeiten, enthält. Mit der sicheren Entnahmerate ist man auch dann sicher, wenn man am Abend vor dem Ausbruch der Weltwirtschaftskrise sein Rentnerdasein beginnt. Falls Du der Meinung bist, dass es sich hierbei um ein bisschen zu viel Sicherheit handelt, dann stimme ich zu, und habe deshalb auch noch den Verlauf für etwas höhere Fehlerwahrscheinlichkeiten abgebildet. Die wahre sichere Entnahmerate liegt demnach bei 3%-3,5%.

Ich hoffe ich habe Dich an dieser Stelle nicht hinsichtlich Deiner Planung verunsichert. Eine geringere Entnahmerate geht ja auch immer mit einem höheren Sparziel einher. Während Du gemäß der 4% Regel das 25-fache Deiner jährlichen Ausgaben ansparen musst, sind es bei 3% bereits das 33-fache. Die Latte der finanziellen Freiheit hängt deutlich höher. Falls Du also bisher mit der 4%-Regel geplant hast und ich Dich nun an der Stelle verunsichert habe, dann sei mir bitte nicht böse und warte ab. Denn in den kommenden Artikeln in dieser Serie werden wir untersuchen wie sich weitere wichtige Effekte wie z.B. Wechselkursschwankungen oder Steuern auf die Entnahmerate auswirken. Und ich kann Dir jetzt schon versprechen, dass wir dabei durchaus auch positives zu Tage fördern werden. In jedem Fall macht es Sinn sich nicht selbst zu betrügen, sondern die eigene  Lebensplanung auf einem realistischen Fundament zu basieren.

Wenn Du mehr über die 4% Regel wissen willst, dann empfehle ich Dir auch die anderen Teile dieser Serie zu lesen:

Teil 2: hier untersuche ich wie sich das Wechselkursrisiko auf die sichere Entnahmerate auswirkt.

Teil 3: hier zeige ich wie sich Steuern auf die sichere Entnahmerate auswirken.